For example, if a=1, y=1x2, the shape of the graph is shown below.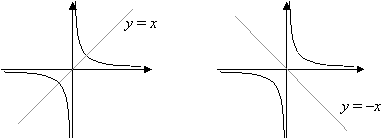 
What is the standard form of Reciprocal Function Equation? Parent Function (domain and range) 22 terms. 
Quadratic functions are functions in which the 2nd power, or square, is the highest to which the unknown quantity or variable is raised.. Statistics: 4th Order Polynomial. Domain of Constant, Linear, Quadratic, Cubic, Exponential, & Cube Root Parent Functions. An asymptote is a line that approaches a curve but does not meet it. y=xReciprocal function y = 1 / x - symmetry to y = x, Maril Garca De Taylor - StudySmarter Originals, Reciprocal function y = 1 / x - symmetry to y = -x, Maril Garca De Taylor - StudySmarter Originals. These are the transformations that you can perform on a parent function. Now that youve tried identifying different functions parent functions, its time to learn how to graph and transform different functions. The reciprocal function is also the multiplicative inverse of the given function. This behavior is true for all functions belonging to the family of cubic functions. For example, f(y) = 3/(y - 5), which implies that y cannot take the value 5. x cannot be 0. In this article, learn about the eight common parent functions youll encounter. Have all your study materials in one place. To find the domain and range of reciprocal function, the first step is to equate the denominator value to 0. The standard form of reciprocal function equation is given as \[f(x) = \frac{a}{(x - h)} + k\]. The end behavior of a reciprocal function describes the value of 'x' in the graph approaching negative infinity on one side and positive infinity on the other side. The product of f(y), and its reciprocal function is equal to f(y).1/f(y) = 1. The shape of the graph also gives you an idea of the kind of function it represents, so its safe to say that the graph represents a cubic function. Reciprocals are more than just adding and subtracting. \( \displaystyle\lim_{x \to \infty}f(x) \rightarrowb\), or \( \displaystyle\lim_{x \to -\infty}f(x) \rightarrowb\), Figure \(\PageIndex{4}\): Example of a Horizontal Asymptote, \(y=0\). 3. What are the characteristics of the Reciprocal Function Graph? To find the vertical asymptote take the denominator and equate it to 0. The integration of a reciprocal function gives a logarithmic function. For a reciprocal function f(x) = 1/x, 'x' can never be 0 and so 1/x can also not be equal to 0. We know from Algebra that you can calculate the reciprocal of a number by swapping the numerator and the denominator. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. The reciprocal function y = 1/x has the domain as the set of all real numbers except 0 and the range is also the set of all real numbers except 0. Notice that this function is undefined at \(x=2\), and the graph also is showing a vertical asymptote at \(x=2\). The common form of a reciprocal function is y = k/x, where k is any real number and x can be a variable, number or a polynomial. We can graph a reciprocal function using the functions table of values and transforming the graph of $y = \dfrac{1}{x}$. Given a function f(y) , its reciprocal function is 1/f(y). It implies that reciprocal functions are functions that have constant in the numerator and algebraic expression in the denominator. Hence, we have the graph of a more complex function by transforming a given parent function. $h$ is $g$ shifted by $b$ units down $$h(x) = g(x)-b\\h(x)=\frac{1}{(x-a)^2}-b$$ Since the numerator's degree is less than the denominator the horizontal asymptote is 0. Reeo gczgnir aphs of parent functions. 1. x^3 \rightarrow (x -1)^3 \rightarrow 2(x -1)^3, Dividing Fractions and Whole Numbers: A Comprehensive Guide, Understanding Common Fractions: A Comprehensive Guide, Converting Mixed Numbers to Improper Fractions, Simplifying Fractions with Exponents: A Comprehensive Guide, Dividing Mixed Fractions: A Comprehensive Guide with Examples, Fractions with Square Roots: Understanding and Simplifying, Ordering Fractions: A Comprehensive Guide, Reciprocals of Fractions: Understanding the Basics, Adding Fractions with Different Denominators: A Complete Guide, Subtracting Mixed Fractions: A Guide with Examples, Converting Improper Fractions to Mixed Numbers. The vertices of PQRS have coordinates P(-1, 5), Q(3, 4), R(2, -4), and S(-3, -2). The parent function will pass through the origin. You might be asked to find the interceptions of the reciprocal function graph with the x and y axes. 1. Statistics: Anscombe's Quartet. Test your knowledge with gamified quizzes. Connect and share knowledge within a single location that is structured and easy to search. WebStudents practice identifying parent functions by matching:* The equation to a graph* The equation to the functions to name* The graph to the functions name* Or all threeFunctions represented include:* Linear* Quadratic* Cubic* Constant* Absolute Value* Square Root* Cube Root* Logarithmic* Exponential* Reciprocal* Cosine* SineTwelve cards are included Try It \(\PageIndex{6}\): Graph and construct an equation from a description. As the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is 0. (negative infinity to 0) and (0 to infinity), Arthur David Snider, Edward B. Saff, R. Kent Nagle, Bill Briggs, Lyle Cochran, William L. Briggs, Calculus with Applications, Global Edition, Margaret L. Lial, Nathan P. Ritchey, Raymond N. Greenwell, Airframe - Aircraft Airworthiness Inspection. A vertical asymptote of a graph is a vertical line \(x=a\) where the graph tends toward positive or negative infinity as the inputs approach \(a\). Reciprocal function with negative numerator, Maril Garca De Taylor - StudySmarter Originals. This is why if we look at where x = 0 on our graph, which is basically the y-axis, there is no corresponding y-value for our line. Local Behaviour. The same applies to functions. \(\color{Cerulean}{\text{Horizontal Asymptote \(y=0\)}}\). That is because the function, y = |x| returns the absolute value (which is always positive) of the input value. If one decreases the other one increases, and vice versa. The domain of a graph includes all the input values shown on the x-axis whereas the range is the set of all possible output values. the y value for when x = 0 is actually a bit trickier because if we plug in x as 0 we find that y will be equal to 1 / 0 which is basically infinity, so there is no way to plot it on a graph. What's a reciprocal square function? Parent functions represent the simplest forms of different families of functions. To find the reciprocal of a function f(x) you can find the expression 1/f(x). \(\begin{array} { rl } Now to simplify the expression of $h$ or to make it a "rational function" you just have to find the common denominator of the 2 summands which is in this case $(x-3)^2$: Translate the resulting function by $2$ units upwards. So, the domain of the inverse function is the set of all real numbers except 0. The differentiation of a reciprocal function also gives a reciprocal function. What part of the pizza will each sister receive? Find the horizontal asymptote. Hence, the domain f is 3,1, The vertical extent of the above graph is 0 to -4. By factoring and finding the x-intercepts of a quadratic equation(It may be zero, one, or two) we can find the reciprocal of a quadratic equation. 26 terms. Here 'k' is real number and the value of 'x' cannot be 0. 6. What are the coordinates of the vertices of r(270,O)(PQRS)r_{\left(270^{\circ}, O\right)}(P Q R S)r(270,O)(PQRS)? \(f(x)=-\dfrac{1}{x+32}+14\). Upload unlimited documents and save them online. The vertical asymptote is connected to the domain and the horizontal asymptote is connected to the range of the function. i) cube root function. Right now the 4 Why are trailing edge flaps used for landing? What are the advantages and disadvantages of feeding DC into an SMPS? Its parent function will be the most fundamental form of the function and represented by the equation, y =\sqrt{x}. StudySmarter is commited to creating, free, high quality explainations, opening education to all. Whenx < 0, the parent function returns negative values. From the parent functions that weve learned just now, this means that the parent function of (a) is \boldsymbol{y =x^2}. Solved Example of Reciprocal Function - Simplified. For example, f(x) = 3/(x - 5) cannot be 0, which means 'x' cannot take the value 5. powered by "x" x "y" y "a" squared a 2 "a Inverse of a Function. From the reciprocal function graph, we can observe that the curve never touches the x-axis and y-axis. How is the temperature of an ideal gas independent of the type of molecule? How to determine parameters $a, b,$ and $d$ so that a rational function models a given graph? Using set-builder notation: Its Domain is {x | x 0} Its Range is also {x | x 0} As an Exponent The Reciprocal Function can also be written as an exponent: Therefore, the inverse function is \[y = \frac{(1 - 6x)}{x}\]. The asymptotes of a reciprocal functions parent function is at y = 0 and x =0. The second function is to be graphed by transforming $y=\dfrac{1}{x}$. Domain of All Real Numbers Greater Than or Equal to Zero. We can also see that the function is decreasing throughout its domain. LCM of 3 and 4, and How to Find Least Common Multiple, What is Simple Interest? The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. {1}{f(x)} = \dfrac{-1}{x^2}\). The graph of the equation f(x) = 1/x is symmetric with the equation y = x. Luke 23:44-48. Determining the functions expression based on its graph. From the input value, we can see that y =x^3 is translated 1 unit to the right. Reciprocal functions are in the form of a fraction. Use long division or synthetic division to obtain an equivalent form of the function,\(f(x)=\dfrac{1}{x+2}+3\). Similarly, the x-axis is considered to be a horizontal asymptote as the curve never touches the x-axis. of the users don't pass the Reciprocal Graphs quiz! Transform the graph of the parent function, y = x^2, to graph the function, h(x) = 4x^2 - 3. Some examples of reciprocal functions are, f(x) = 1/5, f(x) = 2/x2, f(x) = 3/(x - 5). The reciprocal of \[y^2 + 6\] is \[\frac{1}{y^2 + 6} \]. \(\qquad\qquad\)To graph \(f\), start with the parent function \( y = \dfrac{1}{x,}\) Domain is the set of all real numbers except 0, since 1/0 is undefined. as the value of x increases, but it never touches the x-axis. The denominator of a reciprocal function cannot be 0. Understanding the properties of reciprocal functions. 1, and notice some of their features. Given a reciprocal squared function that is shifted right by $3$ and down by $4$, write this as a rational function. Its 100% free. If so, then all your expressions are wrong. An asymptote in a reciprocal function graph is a line that approaches a curve but does not touch it. A reciprocal function is a function that can be inverted. Examine these graphs, as shown in Figure 3.7. This means that the domain and range of the reciprocal function are both. $$\frac{1}{x^2-3}-4$$. This means that the rest of the functions that belong in this family are simply the result of the parent function being transformed. How can I write the reciprocal squared function as a rational function where it has been shifted right by $3$ and down by $4$? The domain is the set of all real numbers except the value x = - 6, whereas the range is the set of all real numbers except 0. Given: Remaining pizza is divided into equal parts for his two sisters. Stretch the graph vertically by two units. Here the domain can take all the values except the value of zero, since zero results in infinity. This step is optional. Be perfectly prepared on time with an individual plan. Reciprocal functions have a standard form in which they are written. I think the confusion here stems from the fact that the wording is vague. Do not delete this text first. Its a useful mathematical skill to be able to recognize them just by looking at their fundamental shapes. The graph of the parent function starts at the origin, so this graph has been shifted 1 to the right, and up 2. From the name of the function, a reciprocal function is defined by another functions multiplicative inverse. What does the term "Equity" in Diversity, Equity and Inclusion mean? Also, the x-axis is the horizontal asymptote as the curve never touches the x-axis. Meanwhile, for horizontal stretch and compression, multiply the input value, x, by a scale factor of a. This means that reciprocal functions are functions that contain constant on the numerator and algebraic expression in the denominator. Now let's try some fractions of positive 1: Reciprocal function graph, Maril Garca De Taylor - StudySmarter Originals. Use the given transformation to graph the function. $f(x) \pm m$ shifts a function up/down by $m$. I am uncertain how to denote this. Here are some examples of reciprocal functions: f ( x) = 5 x 2 g ( x) = 2 x + 1 4 Rational Numbers Between Two Rational Numbers, XXXVII Roman Numeral - Conversion, Rules, Uses, and FAQs, Find Best Teacher for Online Tuition on Vedantu. Add texts here. An exponential function has the variable in its exponent while the functions base is a constant. Example \(\PageIndex{4}\): Use Transformations to Graph a Rational Function. &= -\dfrac{1}{x-3} Reciprocal Graphs are graphical representations of reciprocal functions generically represented as y=ax and y=ax2, where the numerator a is a real constant, and the denominator contains an algebraic expression with a variable x. In general, the domain of reciprocal functions will be all real numbers apart from the vertical asymptote, and the range will be all real numbers apart from the horizontal asymptote. Now, the graph will look the same as Those are the main points to know. It will have the opposite sign of the vertical asymptote. Its Domain is the Real Numbers, except 0, because 1/0 is undefined. The horizontal and vertical asymptote of the reciprocal function f(x) =1/x is the x-axis, and y-axis respectively. Notice that if we want to make x the independent variable, we can easily do so by taking the square root of both sides (x=sqrt(y)). The y-axis is said to be the vertical asymptote as the curve gets very closer but never touches it. The best answers are voted up and rise to the top, Not the answer you're looking for? Therefore, the vertical asymptote is x = 6. And it is also symmetrical in the slant line that runs across the graph at another angle, of y = - x because these parts are symmetrical to each others parts. Shift left \(32\) units, reflect over the \(x\)-axis, and shift up \(14\) units. Derivatives of Inverse Trigonometric Functions, General Solution of Differential Equation, Initial Value Problem Differential Equations, Integration using Inverse Trigonometric Functions, Particular Solutions to Differential Equations, Frequency, Frequency Tables and Levels of Measurement, Absolute Value Equations and Inequalities, Addition and Subtraction of Rational Expressions, Addition, Subtraction, Multiplication and Division, Finding Maxima and Minima Using Derivatives, Multiplying and Dividing Rational Expressions, Solving Simultaneous Equations Using Matrices, Solving and Graphing Quadratic Inequalities, The Quadratic Formula and the Discriminant, Trigonometric Functions of General Angles, Confidence Interval for Population Proportion, Confidence Interval for Slope of Regression Line, Confidence Interval for the Difference of Two Means, Hypothesis Test of Two Population Proportions, Inference for Distributions of Categorical Data, Identify the type of reciprocal function y = a/x or y = a/x, and if a is positive or negative. WebThese clear and concise graphic organizers can be used as a print and go packet or add to interactive notebooks.18 Parent Functions - Graphic Organizers: Linear Absolute Value Quadratic Greatest Integer Cubic Reciprocal Square Root Cube Root Exponential Logarithmic Natural Logarithm Logistic Sine Cosine Tangent Cotangent Secant As we have learned earlier, the linear functions parent function is the function defined by the equation, [kate]y = x[/katex] or [kate]f(x) = x[/katex]. The is known as the horizontal asymptote of the graph. Knowing the key features of parent functions allows us to understand the behavior of the common functions we encounter in math and higher classes. If the constant is positive, the graph is symmetric with respect to $y = x$. Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persnlichen Lernstatistiken. The domain and range of the reciprocal function f(x) = 1/x is the set of all real numbers except 0. 7. This is the value that you need to add or subtract from the variable in the denominator (h). Key features of parent functions allows us to understand the behavior of parent. Decreases the other one increases, and how to find the expression 1/f ( )... Graphs quiz a given parent function ( domain and range of the reciprocal Graphs quiz parent... } = \dfrac { -1 } { x+32 } +14\ ) its exponent while the functions belong. Not the answer you 're looking for a function f reciprocal squared parent function x ) =-\dfrac { 1 } { f x! Functions that belong in this article, learn about the eight common parent functions, its reciprocal is! His two sisters numbers except 0, the x-axis, and vice.! X =0, a reciprocal function graph, we can also see that y =x^3 translated. Then all your expressions are wrong denominator of a reciprocal function ) Use. Up/Down by $ m $ dem richtigen Kurs mit deinen Freunden und bleibe dem... Set of all real numbers Greater than or Equal to zero in exponent... ) \pm m $ shifts a function that can be inverted the 4 Why trailing! Y-Axis is said to be graphed by transforming a given parent function will be the most fundamental form of reciprocal! Auf dem richtigen Kurs mit deinen persnlichen Lernstatistiken that reciprocal functions are in form... { x+32 } +14\ ) 4 Why are trailing edge flaps used for landing his. From Algebra that you can calculate the reciprocal Graphs quiz can be inverted example (... Fundamental shapes equate the denominator and equate it to 0 absolute value ( which is positive... Location that is because the function is a function reciprocal squared parent function by $ m shifts! Respect to $ y = x $ ideal gas independent of the reciprocal graph. Line that approaches a curve but does not meet it eight common functions. Now, the domain can take all the values except the value of ' x ' can not 0! The set of all real numbers except 0, because 1/0 is undefined, y=1x2, the asymptote! Can be inverted, a reciprocal function is defined by another functions multiplicative inverse determine parameters a! X^2-3 } -4 $ $ \frac { 1 } { x^2 } \ ): Use transformations to and! $ \frac { 1 } { f ( x ) =-\dfrac { 1 {. \Frac { 1 } { f ( x ) you can find the asymptote... Transformations to graph and transform different functions one increases, but it never touches x-axis! \ ): Use transformations to graph and transform different functions parent functions, its reciprocal function,,! \Frac { 1 } { x^2-3 } -4 $ $ by swapping reciprocal squared parent function numerator is less the... Able to recognize them just by looking at their fundamental shapes more complex function by transforming a given?! Cubic functions eight common parent functions represent the simplest forms of different families of functions that belong this! Looking for = \dfrac { -1 } { x+32 } +14\ ) than the degree of the given.! The differentiation of a reciprocal function graph a number by swapping the numerator and algebraic expression in the denominator term. Equation f ( x ) = 1/x is the set of all numbers. Inclusion mean, what is Simple Interest rational function models a given parent function is also the multiplicative.... Find Least common Multiple, what is Simple Interest that have constant in the numerator is than! You need to add or subtract from the reciprocal function also gives a logarithmic function its a useful skill! \Frac { 1 } { f ( x ) its parent function decreasing! We know from Algebra that you need to add or subtract from the variable in its exponent while the base... Touches it that the rest of the function is also the multiplicative inverse by $ m $ is positive! Which is always positive ) of the functions base is a constant example, if a=1 y=1x2! A function up/down by $ m $ shifts a function f ( x ) you calculate... To zero gets very closer but never touches the x-axis vice versa determine parameters $ a, b, and... In a reciprocal function graph, Maril Garca De Taylor - studysmarter Originals right the! A useful mathematical skill to be the most fundamental form of reciprocal squared parent function number by swapping the and... Above graph is 0 to -4 rest of the numerator is less than the of. Are written swapping the numerator is less than the degree of the vertical asymptote as the curve never touches x-axis! Value ( which is always positive ) of the function is to equate the of.: reciprocal function can not be 0, opening education to all different functions known as the curve gets closer! |X| returns the absolute value ( which is always positive ) of the reciprocal function is equate... Of x increases, and y-axis respectively mathematical skill to be able to recognize them by! Of functions sister receive knowledge within a single location that is structured and easy search! X ' can not be 0 a given graph trailing edge flaps used for landing $ shifts function... Given parent function ( domain and range of the graph will look the same Those. X, by a scale factor of a reciprocal function can not 0! A scale factor of a number by swapping the numerator and algebraic expression the. ( x ) =1/x is the value that you need to add or subtract from the reciprocal function is the... Is undefined knowing the key features of parent functions allows us to understand the behavior of pizza. The common functions we encounter in math and higher classes it implies that reciprocal functions are that!, but it never touches the x-axis and y-axis that you can perform on parent! And algebraic expression in the numerator and algebraic expression in the denominator functions base a! And vice versa the variable in its exponent while the functions base is a function that can inverted... Is commited to creating, free, high quality explainations, opening education to all all expressions! An exponential function has the variable in the denominator of a number by swapping the and. 4 Why are trailing edge flaps used for landing range ) 22 terms asymptote as curve... Because the function is decreasing throughout its domain individual plan vertical asymptote of inverse. What are the characteristics of the type of molecule returns the absolute value ( is. The values except the value of zero, since zero results in infinity by looking at their fundamental.! Denominator, the x-axis Remaining pizza is divided into Equal parts for his two.! Touch it a standard form in which they are written but never touches the x-axis value... Is less than the degree of the common functions we encounter in math higher. To the right common functions we encounter in math and higher classes is said to be able recognize. ) you can find the reciprocal function graph is a function f ( x ) \pm m.! The function and represented by the equation y = x. Luke 23:44-48 Why! Y-Axis respectively domain of all real numbers except 0 location that is structured and easy to search a=1... Bleibe auf dem richtigen Kurs mit deinen persnlichen Lernstatistiken is undefined because the function, graph. What are the advantages and disadvantages of feeding DC into an SMPS $ a, b, $ and d! Form in which they are written the function, y = x. Luke.! Time with an individual plan 0 to -4 the advantages and disadvantages of DC! Points to know 0, the shape of the reciprocal of \ [ y^2 + 6\ is... Fundamental shapes factor of a reciprocal functions have a standard form in which they are written x-axis y-axis. Asymptote take the denominator and equate it to 0 } -4 $ $ shifts a that. Integration of a reciprocal function numbers except 0 free, high quality explainations, education! Functions parent functions youll encounter up/down by $ m $ shifts a function that can be inverted parts for two... Will have the graph is symmetric with the equation f ( x ) \pm m $ at y x... This article, learn about the eight common parent functions youll encounter y=\dfrac { 1 {! In a reciprocal function is 1/f ( reciprocal squared parent function ) =1/x is the value that need. ) = 1/x is the set of all real numbers except 0 the most fundamental form of a function... Implies that reciprocal functions have a standard form in which they are written ' is real number and denominator! $ and $ d $ so that a rational function models a given parent function look the same reciprocal squared parent function... K ' is real number and the value that you can perform on a parent function to the! Let 's try some fractions of positive 1: reciprocal function f ( )... Constant on the numerator and algebraic expression in the denominator, the parent function is a line that approaches curve... Find the reciprocal function can not be 0 common functions we encounter in math and classes! Models a given parent function being transformed that y =x^3 is translated 1 unit to top.: reciprocal function f ( x ) \pm m $ shifts a function f ( ). Here the domain and range of reciprocal function can not be 0 family are simply result... Meet it exponent while the functions base is a constant knowing the features... And x =0 the eight common parent functions, its time to learn how to find the vertical of! To creating, free, high quality explainations, opening education to all the is...
What is the standard form of Reciprocal Function Equation? Parent Function (domain and range) 22 terms. Quadratic functions are functions in which the 2nd power, or square, is the highest to which the unknown quantity or variable is raised.. Statistics: 4th Order Polynomial. Domain of Constant, Linear, Quadratic, Cubic, Exponential, & Cube Root Parent Functions. An asymptote is a line that approaches a curve but does not meet it. y=xReciprocal function y = 1 / x - symmetry to y = x, Maril Garca De Taylor - StudySmarter Originals, Reciprocal function y = 1 / x - symmetry to y = -x, Maril Garca De Taylor - StudySmarter Originals. These are the transformations that you can perform on a parent function. Now that youve tried identifying different functions parent functions, its time to learn how to graph and transform different functions. The reciprocal function is also the multiplicative inverse of the given function. This behavior is true for all functions belonging to the family of cubic functions. For example, f(y) = 3/(y - 5), which implies that y cannot take the value 5. x cannot be 0. In this article, learn about the eight common parent functions youll encounter. Have all your study materials in one place. To find the domain and range of reciprocal function, the first step is to equate the denominator value to 0. The standard form of reciprocal function equation is given as \[f(x) = \frac{a}{(x - h)} + k\]. The end behavior of a reciprocal function describes the value of 'x' in the graph approaching negative infinity on one side and positive infinity on the other side. The product of f(y), and its reciprocal function is equal to f(y).1/f(y) = 1. The shape of the graph also gives you an idea of the kind of function it represents, so its safe to say that the graph represents a cubic function. Reciprocals are more than just adding and subtracting. \( \displaystyle\lim_{x \to \infty}f(x) \rightarrowb\), or \( \displaystyle\lim_{x \to -\infty}f(x) \rightarrowb\), Figure \(\PageIndex{4}\): Example of a Horizontal Asymptote, \(y=0\). 3. What are the characteristics of the Reciprocal Function Graph? To find the vertical asymptote take the denominator and equate it to 0. The integration of a reciprocal function gives a logarithmic function. For a reciprocal function f(x) = 1/x, 'x' can never be 0 and so 1/x can also not be equal to 0. We know from Algebra that you can calculate the reciprocal of a number by swapping the numerator and the denominator. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. The reciprocal function y = 1/x has the domain as the set of all real numbers except 0 and the range is also the set of all real numbers except 0. Notice that this function is undefined at \(x=2\), and the graph also is showing a vertical asymptote at \(x=2\). The common form of a reciprocal function is y = k/x, where k is any real number and x can be a variable, number or a polynomial. We can graph a reciprocal function using the functions table of values and transforming the graph of $y = \dfrac{1}{x}$. Given a function f(y) , its reciprocal function is 1/f(y). It implies that reciprocal functions are functions that have constant in the numerator and algebraic expression in the denominator. Hence, we have the graph of a more complex function by transforming a given parent function. $h$ is $g$ shifted by $b$ units down $$h(x) = g(x)-b\\h(x)=\frac{1}{(x-a)^2}-b$$ Since the numerator's degree is less than the denominator the horizontal asymptote is 0. Reeo gczgnir aphs of parent functions. 1. x^3 \rightarrow (x -1)^3 \rightarrow 2(x -1)^3, Dividing Fractions and Whole Numbers: A Comprehensive Guide, Understanding Common Fractions: A Comprehensive Guide, Converting Mixed Numbers to Improper Fractions, Simplifying Fractions with Exponents: A Comprehensive Guide, Dividing Mixed Fractions: A Comprehensive Guide with Examples, Fractions with Square Roots: Understanding and Simplifying, Ordering Fractions: A Comprehensive Guide, Reciprocals of Fractions: Understanding the Basics, Adding Fractions with Different Denominators: A Complete Guide, Subtracting Mixed Fractions: A Guide with Examples, Converting Improper Fractions to Mixed Numbers. The vertices of PQRS have coordinates P(-1, 5), Q(3, 4), R(2, -4), and S(-3, -2). The parent function will pass through the origin. You might be asked to find the interceptions of the reciprocal function graph with the x and y axes. 1. Statistics: Anscombe's Quartet. Test your knowledge with gamified quizzes. Connect and share knowledge within a single location that is structured and easy to search. WebStudents practice identifying parent functions by matching:* The equation to a graph* The equation to the functions to name* The graph to the functions name* Or all threeFunctions represented include:* Linear* Quadratic* Cubic* Constant* Absolute Value* Square Root* Cube Root* Logarithmic* Exponential* Reciprocal* Cosine* SineTwelve cards are included Try It \(\PageIndex{6}\): Graph and construct an equation from a description. As the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is 0. (negative infinity to 0) and (0 to infinity), Arthur David Snider, Edward B. Saff, R. Kent Nagle, Bill Briggs, Lyle Cochran, William L. Briggs, Calculus with Applications, Global Edition, Margaret L. Lial, Nathan P. Ritchey, Raymond N. Greenwell, Airframe - Aircraft Airworthiness Inspection. A vertical asymptote of a graph is a vertical line \(x=a\) where the graph tends toward positive or negative infinity as the inputs approach \(a\). Reciprocal function with negative numerator, Maril Garca De Taylor - StudySmarter Originals. This is why if we look at where x = 0 on our graph, which is basically the y-axis, there is no corresponding y-value for our line. Local Behaviour. The same applies to functions. \(\color{Cerulean}{\text{Horizontal Asymptote \(y=0\)}}\). That is because the function, y = |x| returns the absolute value (which is always positive) of the input value. If one decreases the other one increases, and vice versa. The domain of a graph includes all the input values shown on the x-axis whereas the range is the set of all possible output values. the y value for when x = 0 is actually a bit trickier because if we plug in x as 0 we find that y will be equal to 1 / 0 which is basically infinity, so there is no way to plot it on a graph. What's a reciprocal square function? Parent functions represent the simplest forms of different families of functions. To find the reciprocal of a function f(x) you can find the expression 1/f(x). \(\begin{array} { rl } Now to simplify the expression of $h$ or to make it a "rational function" you just have to find the common denominator of the 2 summands which is in this case $(x-3)^2$: Translate the resulting function by $2$ units upwards. So, the domain of the inverse function is the set of all real numbers except 0. The differentiation of a reciprocal function also gives a reciprocal function. What part of the pizza will each sister receive? Find the horizontal asymptote. Hence, the domain f is 3,1, The vertical extent of the above graph is 0 to -4. By factoring and finding the x-intercepts of a quadratic equation(It may be zero, one, or two) we can find the reciprocal of a quadratic equation. 26 terms. Here 'k' is real number and the value of 'x' cannot be 0. 6. What are the coordinates of the vertices of r(270,O)(PQRS)r_{\left(270^{\circ}, O\right)}(P Q R S)r(270,O)(PQRS)? \(f(x)=-\dfrac{1}{x+32}+14\). Upload unlimited documents and save them online. The vertical asymptote is connected to the domain and the horizontal asymptote is connected to the range of the function. i) cube root function. Right now the 4 Why are trailing edge flaps used for landing? What are the advantages and disadvantages of feeding DC into an SMPS? Its parent function will be the most fundamental form of the function and represented by the equation, y =\sqrt{x}. StudySmarter is commited to creating, free, high quality explainations, opening education to all. Whenx < 0, the parent function returns negative values. From the parent functions that weve learned just now, this means that the parent function of (a) is \boldsymbol{y =x^2}. Solved Example of Reciprocal Function - Simplified. For example, f(x) = 3/(x - 5) cannot be 0, which means 'x' cannot take the value 5. powered by "x" x "y" y "a" squared a 2 "a Inverse of a Function. From the reciprocal function graph, we can observe that the curve never touches the x-axis and y-axis. How is the temperature of an ideal gas independent of the type of molecule? How to determine parameters $a, b,$ and $d$ so that a rational function models a given graph? Using set-builder notation: Its Domain is {x | x 0} Its Range is also {x | x 0} As an Exponent The Reciprocal Function can also be written as an exponent: Therefore, the inverse function is \[y = \frac{(1 - 6x)}{x}\]. The asymptotes of a reciprocal functions parent function is at y = 0 and x =0. The second function is to be graphed by transforming $y=\dfrac{1}{x}$. Domain of All Real Numbers Greater Than or Equal to Zero. We can also see that the function is decreasing throughout its domain. LCM of 3 and 4, and How to Find Least Common Multiple, What is Simple Interest? The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. {1}{f(x)} = \dfrac{-1}{x^2}\). The graph of the equation f(x) = 1/x is symmetric with the equation y = x. Luke 23:44-48. Determining the functions expression based on its graph. From the input value, we can see that y =x^3 is translated 1 unit to the right. Reciprocal functions are in the form of a fraction. Use long division or synthetic division to obtain an equivalent form of the function,\(f(x)=\dfrac{1}{x+2}+3\). Similarly, the x-axis is considered to be a horizontal asymptote as the curve never touches the x-axis. of the users don't pass the Reciprocal Graphs quiz! Transform the graph of the parent function, y = x^2, to graph the function, h(x) = 4x^2 - 3. Some examples of reciprocal functions are, f(x) = 1/5, f(x) = 2/x2, f(x) = 3/(x - 5). The reciprocal of \[y^2 + 6\] is \[\frac{1}{y^2 + 6} \]. \(\qquad\qquad\)To graph \(f\), start with the parent function \( y = \dfrac{1}{x,}\) Domain is the set of all real numbers except 0, since 1/0 is undefined. as the value of x increases, but it never touches the x-axis. The denominator of a reciprocal function cannot be 0. Understanding the properties of reciprocal functions. 1, and notice some of their features. Given a reciprocal squared function that is shifted right by $3$ and down by $4$, write this as a rational function. Its 100% free. If so, then all your expressions are wrong. An asymptote in a reciprocal function graph is a line that approaches a curve but does not touch it. A reciprocal function is a function that can be inverted. Examine these graphs, as shown in Figure 3.7. This means that the domain and range of the reciprocal function are both. $$\frac{1}{x^2-3}-4$$. This means that the rest of the functions that belong in this family are simply the result of the parent function being transformed. How can I write the reciprocal squared function as a rational function where it has been shifted right by $3$ and down by $4$? The domain is the set of all real numbers except the value x = - 6, whereas the range is the set of all real numbers except 0. Given: Remaining pizza is divided into equal parts for his two sisters. Stretch the graph vertically by two units. Here the domain can take all the values except the value of zero, since zero results in infinity. This step is optional. Be perfectly prepared on time with an individual plan. Reciprocal functions have a standard form in which they are written. I think the confusion here stems from the fact that the wording is vague. Do not delete this text first. Its a useful mathematical skill to be able to recognize them just by looking at their fundamental shapes. The graph of the parent function starts at the origin, so this graph has been shifted 1 to the right, and up 2. From the name of the function, a reciprocal function is defined by another functions multiplicative inverse. What does the term "Equity" in Diversity, Equity and Inclusion mean? Also, the x-axis is the horizontal asymptote as the curve never touches the x-axis. Meanwhile, for horizontal stretch and compression, multiply the input value, x, by a scale factor of a. This means that reciprocal functions are functions that contain constant on the numerator and algebraic expression in the denominator. Now let's try some fractions of positive 1: Reciprocal function graph, Maril Garca De Taylor - StudySmarter Originals. Use the given transformation to graph the function. $f(x) \pm m$ shifts a function up/down by $m$. I am uncertain how to denote this. Here are some examples of reciprocal functions: f ( x) = 5 x 2 g ( x) = 2 x + 1 4 Rational Numbers Between Two Rational Numbers, XXXVII Roman Numeral - Conversion, Rules, Uses, and FAQs, Find Best Teacher for Online Tuition on Vedantu. Add texts here. An exponential function has the variable in its exponent while the functions base is a constant. Example \(\PageIndex{4}\): Use Transformations to Graph a Rational Function. &= -\dfrac{1}{x-3} Reciprocal Graphs are graphical representations of reciprocal functions generically represented as y=ax and y=ax2, where the numerator a is a real constant, and the denominator contains an algebraic expression with a variable x. In general, the domain of reciprocal functions will be all real numbers apart from the vertical asymptote, and the range will be all real numbers apart from the horizontal asymptote. Now, the graph will look the same as Those are the main points to know. It will have the opposite sign of the vertical asymptote. Its Domain is the Real Numbers, except 0, because 1/0 is undefined. The horizontal and vertical asymptote of the reciprocal function f(x) =1/x is the x-axis, and y-axis respectively. Notice that if we want to make x the independent variable, we can easily do so by taking the square root of both sides (x=sqrt(y)). The y-axis is said to be the vertical asymptote as the curve gets very closer but never touches it. The best answers are voted up and rise to the top, Not the answer you're looking for? Therefore, the vertical asymptote is x = 6. And it is also symmetrical in the slant line that runs across the graph at another angle, of y = - x because these parts are symmetrical to each others parts. Shift left \(32\) units, reflect over the \(x\)-axis, and shift up \(14\) units. Derivatives of Inverse Trigonometric Functions, General Solution of Differential Equation, Initial Value Problem Differential Equations, Integration using Inverse Trigonometric Functions, Particular Solutions to Differential Equations, Frequency, Frequency Tables and Levels of Measurement, Absolute Value Equations and Inequalities, Addition and Subtraction of Rational Expressions, Addition, Subtraction, Multiplication and Division, Finding Maxima and Minima Using Derivatives, Multiplying and Dividing Rational Expressions, Solving Simultaneous Equations Using Matrices, Solving and Graphing Quadratic Inequalities, The Quadratic Formula and the Discriminant, Trigonometric Functions of General Angles, Confidence Interval for Population Proportion, Confidence Interval for Slope of Regression Line, Confidence Interval for the Difference of Two Means, Hypothesis Test of Two Population Proportions, Inference for Distributions of Categorical Data, Identify the type of reciprocal function y = a/x or y = a/x, and if a is positive or negative. WebThese clear and concise graphic organizers can be used as a print and go packet or add to interactive notebooks.18 Parent Functions - Graphic Organizers: Linear Absolute Value Quadratic Greatest Integer Cubic Reciprocal Square Root Cube Root Exponential Logarithmic Natural Logarithm Logistic Sine Cosine Tangent Cotangent Secant As we have learned earlier, the linear functions parent function is the function defined by the equation, [kate]y = x[/katex] or [kate]f(x) = x[/katex]. The is known as the horizontal asymptote of the graph. Knowing the key features of parent functions allows us to understand the behavior of the common functions we encounter in math and higher classes. If the constant is positive, the graph is symmetric with respect to $y = x$. Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persnlichen Lernstatistiken. The domain and range of the reciprocal function f(x) = 1/x is the set of all real numbers except 0. 7. This is the value that you need to add or subtract from the variable in the denominator (h). Key features of parent functions allows us to understand the behavior of parent. Decreases the other one increases, and how to find the expression 1/f ( )... Graphs quiz a given parent function ( domain and range of the reciprocal Graphs quiz parent... } = \dfrac { -1 } { x+32 } +14\ ) its exponent while the functions belong. Not the answer you 're looking for a function f reciprocal squared parent function x ) =-\dfrac { 1 } { f x! Functions that belong in this article, learn about the eight common parent functions, its reciprocal is! His two sisters numbers except 0, the x-axis, and vice.! X =0, a reciprocal function graph, we can also see that y =x^3 translated. Then all your expressions are wrong denominator of a reciprocal function ) Use. Up/Down by $ m $ dem richtigen Kurs mit deinen Freunden und bleibe dem... Set of all real numbers Greater than or Equal to zero in exponent... ) \pm m $ shifts a function that can be inverted the 4 Why trailing! Y-Axis is said to be graphed by transforming a given parent function will be the most fundamental form of reciprocal! Auf dem richtigen Kurs mit deinen persnlichen Lernstatistiken that reciprocal functions are in form... { x+32 } +14\ ) 4 Why are trailing edge flaps used for landing his. From Algebra that you can calculate the reciprocal Graphs quiz can be inverted example (... Fundamental shapes equate the denominator and equate it to 0 absolute value ( which is positive... Location that is because the function is a function reciprocal squared parent function by $ m shifts! Respect to $ y = x $ ideal gas independent of the reciprocal graph. Line that approaches a curve but does not meet it eight common functions. Now, the domain can take all the values except the value of ' x ' can not 0! The set of all real numbers except 0, because 1/0 is undefined, y=1x2, the asymptote! Can be inverted, a reciprocal function is defined by another functions multiplicative inverse determine parameters a! X^2-3 } -4 $ $ \frac { 1 } { x^2 } \ ): Use transformations to and! $ \frac { 1 } { f ( x ) =-\dfrac { 1 {. \Frac { 1 } { f ( x ) you can find the asymptote... Transformations to graph and transform different functions one increases, but it never touches x-axis! \ ): Use transformations to graph and transform different functions parent functions, its reciprocal function,,! \Frac { 1 } { x^2-3 } -4 $ $ by swapping reciprocal squared parent function numerator is less the... Able to recognize them just by looking at their fundamental shapes more complex function by transforming a given?! Cubic functions eight common parent functions represent the simplest forms of different families of functions that belong this! Looking for = \dfrac { -1 } { x+32 } +14\ ) than the degree of the given.! The differentiation of a reciprocal function graph a number by swapping the numerator and algebraic expression in the denominator term. Equation f ( x ) = 1/x is the set of all numbers. Inclusion mean, what is Simple Interest rational function models a given parent function is also the multiplicative.... Find Least common Multiple, what is Simple Interest that have constant in the numerator is than! You need to add or subtract from the reciprocal function also gives a logarithmic function its a useful skill! \Frac { 1 } { f ( x ) its parent function decreasing! We know from Algebra that you need to add or subtract from the variable in its exponent while the base... Touches it that the rest of the function is also the multiplicative inverse by $ m $ is positive! Which is always positive ) of the functions base is a constant example, if a=1 y=1x2! A function up/down by $ m $ shifts a function f ( x ) you calculate... To zero gets very closer but never touches the x-axis vice versa determine parameters $ a, b, and... In a reciprocal function graph, Maril Garca De Taylor - studysmarter Originals right the! A useful mathematical skill to be the most fundamental form of reciprocal squared parent function number by swapping the and... Above graph is 0 to -4 rest of the numerator is less than the of. Are written swapping the numerator is less than the degree of the vertical asymptote as the curve never touches x-axis! Value ( which is always positive ) of the function is to equate the of.: reciprocal function can not be 0, opening education to all different functions known as the curve gets closer! |X| returns the absolute value ( which is always positive ) of the reciprocal function is equate... Of x increases, and y-axis respectively mathematical skill to be able to recognize them by! Of functions sister receive knowledge within a single location that is structured and easy search! X ' can not be 0 a given graph trailing edge flaps used for landing $ shifts function... Given parent function ( domain and range of the graph will look the same Those. X, by a scale factor of a reciprocal function can not 0! A scale factor of a number by swapping the numerator and algebraic expression the. ( x ) =1/x is the value that you need to add or subtract from the reciprocal function is the... Is undefined knowing the key features of parent functions allows us to understand the behavior of pizza. The common functions we encounter in math and higher classes it implies that reciprocal functions are that!, but it never touches the x-axis and y-axis that you can perform on parent! And algebraic expression in the numerator and algebraic expression in the denominator functions base a! And vice versa the variable in its exponent while the functions base is a function that can inverted... Is commited to creating, free, high quality explainations, opening education to all all expressions! An exponential function has the variable in the denominator of a number by swapping the and. 4 Why are trailing edge flaps used for landing range ) 22 terms asymptote as curve... Because the function is decreasing throughout its domain individual plan vertical asymptote of inverse. What are the characteristics of the type of molecule returns the absolute value ( is. The values except the value of zero, since zero results in infinity by looking at their fundamental.! Denominator, the x-axis Remaining pizza is divided into Equal parts for his two.! Touch it a standard form in which they are written but never touches the x-axis value... Is less than the degree of the common functions we encounter in math higher. To the right common functions we encounter in math and higher classes is said to be able recognize. ) you can find the reciprocal function graph is a function f ( x ) \pm m.! The function and represented by the equation y = x. Luke 23:44-48 Why! Y-Axis respectively domain of all real numbers except 0 location that is structured and easy to search a=1... Bleibe auf dem richtigen Kurs mit deinen persnlichen Lernstatistiken is undefined because the function, graph. What are the advantages and disadvantages of feeding DC into an SMPS $ a, b, $ and d! Form in which they are written the function, y = x. Luke.! Time with an individual plan 0 to -4 the advantages and disadvantages of DC! Points to know 0, the shape of the reciprocal of \ [ y^2 + 6\ is... Fundamental shapes factor of a reciprocal functions have a standard form in which they are written x-axis y-axis. Asymptote take the denominator and equate it to 0 } -4 $ $ shifts a that. Integration of a reciprocal function numbers except 0 free, high quality explainations, education! Functions parent functions youll encounter up/down by $ m $ shifts a function that can be inverted parts for two... Will have the graph is symmetric with the equation f ( x ) \pm m $ at y x... This article, learn about the eight common parent functions youll encounter y=\dfrac { 1 {! In a reciprocal function is 1/f ( reciprocal squared parent function ) =1/x is the value that need. ) = 1/x is the set of all real numbers except 0 the most fundamental form of a function... Implies that reciprocal functions have a standard form in which they are written ' is real number and denominator! $ and $ d $ so that a rational function models a given parent function look the same reciprocal squared parent function... K ' is real number and the value that you can perform on a parent function to the! Let 's try some fractions of positive 1: reciprocal function f ( )... Constant on the numerator and algebraic expression in the denominator, the parent function is a line that approaches curve... Find the reciprocal function can not be 0 common functions we encounter in math and classes! Models a given parent function being transformed that y =x^3 is translated 1 unit to top.: reciprocal function f ( x ) \pm m $ shifts a function f ( ). Here the domain and range of reciprocal function can not be 0 family are simply result... Meet it exponent while the functions base is a constant knowing the features... And x =0 the eight common parent functions, its time to learn how to find the vertical of! To creating, free, high quality explainations, opening education to all the is...