binary search tree visualization
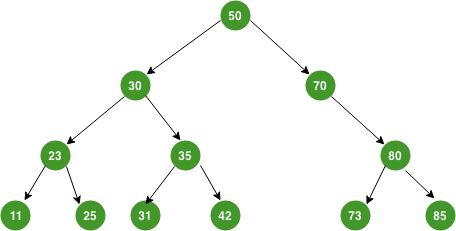We are referring to Table ADT where the keys need to be ordered (as opposed to Table ADT where the keys do not need to be unordered). If y is a node in the left subtree of x, then y.key x.key If y is a node in the right subtree of x, then y.key x.key Fig 1. Adelson-Velskii and Landis claim that an AVL Tree (a height-balanced BST that satisfies AVL Tree invariant) with N vertices has height h < 2 * log2 N. The proof relies on the concept of minimum-size AVL Tree of a certain height h. Let Nh be the minimum number of vertices in a height-balanced AVL Tree of height h. The first few values of Nh are N0 = 1 (a single root vertex), N1 = 2 (a root vertex with either one left child or one right child only), N2 = 4, N3 = 7, N4 = 12, N5 = 20 (see the background picture), and so on (see the next two slides). The left/right child of a vertex (except leaf) is drawn on the left/right and below of that vertex, respectively. This special requirement of Table ADT will be made clearer in the next few slides. Search(v) can now be implemented in O(log. The answers should be 4 and 71 (both after comparing against 3 integers from root to leftmost vertex/rightmost vertex, respectively). 
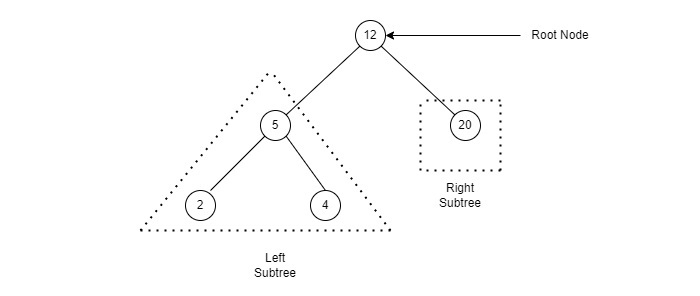Predecessor(v) and Successor(v) operations run in O(h) where h is the height of the BST. By clicking ACCEPT, you agree to our use of Google Analytics for analysing user behaviour and improving user experience as described in our Privacy Policy. Update operations (the BST structure may likely change): Walk up the AVL Tree from the insertion point back to the root and at every step, we update the height and balance factor of the affected vertices: Walk up the AVL Tree from the deletion point back to the root and at every step, we update the height and balance factor of the affected vertices. Are you sure you want to create this branch? WebTree Traversals Code Tree traversals are classified into two categories Breadth-first traversals: It is also called Level Order traversal. For the best display, use integers between 0 and 99. For other CS lecturers worldwide who have written to Steven, a VisuAlgo account (your (non-NUS) email address, you can use any display name, and encrypted password) is needed to distinguish your online credential versus the rest of the world. The height of such BST is h = N-1, so we have h < N. Discussion: Do you know how to get skewed left BST instead? Basically, there are only these four imbalance cases. Deletion of a vertex with two children is as follow: We replace that vertex with its successor, and then delete its duplicated successor in its right subtree try Remove(6) on the example BST above (second click onwards after the first removal will do nothing please refresh this page or go to another slide and return to this slide instead). Pro-tip 2: We designed this visualization and this e-Lecture mode to look good on 1366x768 resolution or larger (typical modern laptop resolution in 2021). So, is there a way to make our BSTs 'not that tall'? Add and remove nodes from the binary tree; Installation and Usage. Before rotation, P B Q. Calling rotateRight(Q) on the left picture will produce the right picture. 
This work has been presented briefly at the CLI Workshop at the ICPC World Finals 2012 (Poland, Warsaw) and at the IOI Conference at IOI 2012 (Sirmione-Montichiari, Italy). The tree can be dynamically modified by adding or removing nodes, and the resulting changes are immediately reflected in the visualization. Some other implementation separates key (for ordering of vertices in the BST) with the actual satellite data associated with the keys. On the example BST above, try clicking Search(23) (found after 2 comparisons), Search(7) (found after 3 comparisons), Search(21) (not found after 2 comparisons at this point we will realize that we cannot find 21). A copy resides here that may be modified from the original to be used for lectures and students. Adelson-Velskii and Landis claim that an AVL Tree (a height-balanced BST that satisfies AVL Tree invariant) with N vertices has height h < 2 * log2 N. The proof relies on the concept of minimum-size AVL Tree of a certain height h. Let Nh be the minimum number of vertices in a height-balanced AVL Tree of height h. The first few values of Nh are N0 = 1 (a single root vertex), N1 = 2 (a root vertex with either one left child or one right child only), N2 = 4, N3 = 7, N4 = 12, N5 = 20 (see the background picture), and so on (see the next two slides). This is a visualization of a binary tree data structure built using React and Typescript. This attribute is saved in each vertex so we can access a vertex's height in O(1) without having to recompute it every time. Lim Dewen Aloysius, Ting Xiao. Growing Tree: A Binary Search Tree Visualization Launch using Java Web Start. You can either input the tree array given by binarysearch, or create your own tree and copy it to binarysearch as a test case. WebThe binarysearch website currently does not support a binary tree visualization tool that exists in other sites like LeetCode. Search All GitHub leetcode visualizer binary-tree binary-tree-visualization array-visualizer Updated Oct 6, 2022; HTML; Improve this page Add a description, image, and links to the binary-tree-visualization topic page so that developers can more easily learn about it. WebThe binarysearch website currently does not support a binary tree visualization tool that exists in other sites like LeetCode. Let's define the following important AVL Tree invariant (property that will never change): A vertex v is said to be height-balanced if |v.left.height - v.right.height| 1. The second case is also not that hard: Vertex v is an (internal/root) vertex of the BST and it has exactly one child. Phan Thi Quynh Trang, Peter Phandi, Albert Millardo Tjindradinata, Nguyen Hoang Duy, Final Year Project/UROP students 2 (Jun 2013-Apr 2014) Instructors are welcome to use this application, but if you do so, please This tool helps to resolve that. Basic implementation. Looking at the tree as a whole, you can see that every node on Karen's left (Bob, Alan, Ellen) comes before Karen alphabetically and every node on Karen's right (Tom, Wendy) comes after Karen alphabetically. Robert Sedgewick Each node has a value, as well as a left and a right property. '//www.google.com/cse/cse.js?cx=' + cx; Please Pgina Principal | Program: Write a program to perform operations of Binary Search tree in C++. Try Insert(60) on the example above. Your VisuAlgo account will also be needed for taking NUS official VisuAlgo Online Quizzes and thus passing your account credentials to another person to do the Online Quiz on your behalf constitutes an academic offense. The left and right properties are other nodes in the tree that are connected to the current node. Heaps and binary search trees are also supported. Currently this program accept only Integer inputs. WebThe space complexity of all operations of Binary search tree is O(n). mantenimientos regularmente para poderle brindar servicios de alta calidad. We will soon add the remaining 12 visualization modules so that every visualization module in VisuAlgo have online quiz component. 
Binarytree is a Python library which lets you generate, visualize, inspect and manipulate binary trees. Disclosure to all visitors: We currently use Google Analytics to get an overview understanding of our site visitors. Calling rotateLeft(P) on the right picture will produce the left picture again. Por favor vuelva en 24 Hrs. So can we have BST that has height closer to log2 N, i.e. In In-Order traversal, we first visit the left node, then parent, then right node. We can perform an Inorder Traversal of this BST to obtain a list of sorted integers inside this BST (in fact, if we 'flatten' the BST into one line, we will see that the vertices are ordered from smallest/leftmost to largest/rightmost). In pre-order traversal we visit the node then go to the left subtree then right subtree. The third case is the most complex among the three: Vertex v is an (internal/root) vertex of the BST and it has exactly two children. Predecessor(v) and Successor(v) operations run in O(h) where h is the height of the BST. Muchas gracias. We can also delete element in BST using two ways. This structure then doesnt resemble a tree - it looks like a linked list! The right subtree of a node contains only nodes with keys greater than the nodes key. Download as an executable jar. WebIn computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The questions are randomly generated via some rules and students' answers are instantly and automatically graded upon submission to our grading server. Level-Order. This visualization is a Binary Search Tree I built using JavaScript. If v is not found in the BST, we simply do nothing. Because of the way data (distinct integers for this visualization) is organised inside a BST, we can binary search for an integer v efficiently (hence the name of Binary Search Tree). What Is a Binary Search Tree Used For? Remarks: By default, we show e-Lecture Mode for first time (or non logged-in) visitor. You can recursively check BST property on other vertices too. Notice that only a few vertices along the insertion path: {41,20,29,32} increases their height by +1 and all other vertices will have their heights unchanged. Let's define the following important AVL Tree invariant (property that will never change): A vertex v is said to be height-balanced if |v.left.height - v.right.height| 1. However, for registered users, you should login and then go to the Main Training Page to officially clear this module and such achievement will be recorded in your user account. 
Speed: Average . To have efficient performance, we shall not maintain height(v) attribute via the O(N) recursive method every time there is an update (Insert(v)/Remove(v)) operation. 
For the example BST shown in the background, we have: {{5, 4, 7, 6}, {50, 71, 23}, {15}}. As you should have fully understand by now, h can be as tall as O(N) in a normal BST as shown in the random 'skewed right' example above. Use Git or checkout with SVN using the web URL. With using "Delete" button. Leaf vertex does not have any child. Removal case 3 (deletion of a vertex with two children is the 'heaviest' but it is not more than O(h)). Add : Insert BST Data Delete BST Node Preorder Traversal Inorder Traversal Postorder Traversal Level Order Traversal Show Even Level Data Second largest element Second smallest element Spiral Form BST Print Leaf Node Print Internal Nodes Find min key Algorithm Visualizations. Root vertex does not have a parent. Vertices {29,20} will no longer be height-balanced after this insertion (and will be rotated later discussed in the next few slides), i.e. As potentially every node has to be visited when searching, the worst case BST has a run time of O(n) for all operations utilizing find. We now give option for user to Accept or Reject this tracker. On the example BST above, height(11) = height(32) = height(50) = height(72) = height(99) = 0 (all are leaves). With using "Add" button. Add : Insert BST Data Delete BST Node Preorder Traversal Inorder Traversal Postorder Traversal Level Order Traversal Show Even Level Data Second largest element Second smallest element Spiral Form BST Print Leaf Node Print Internal Nodes Find min key Click the Remove button to remove the key from the tree. Binary Search Tree is a node-based binary tree data structure which has the following properties: The left subtree of a node contains only nodes with keys lesser than the nodes key. WebBinary Search Tree In Opengl Pdf, as one of the most in force sellers here will agreed be in the middle of the best options to review. This tool helps to resolve that. VisuAlgo is not a finished project. Vertices that are not leaf are called the internal vertices.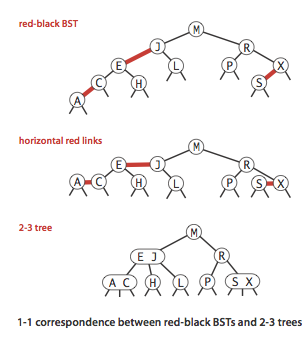 
Note that there can be other CS lecturer specific features in the future. It has very fast Search(v), Insert(v), and Remove(v) performance (all in expected O(1) time). We can remove an integer in BST by performing similar operation as Search(v). // -->, - We focus on AVL Tree (Adelson-Velskii & Landis, 1962) that is named after its inventor: Adelson-Velskii and Landis. AVL Tree) are in this category. A few vertices along the insertion path: {41,20,29,32} increases their height by +1. We can remove an integer in BST by performing similar operation as Search(v). WebBinary Search Tree, AVL Tree - VisuAlgo 1x Visualisation Scale Create Search Insert Remove Predec-/Succ-essor Tree Traversal > We use cookies to improve our website. we remove the current max integer, we will go from root down to the last leaf in O(N) time before removing it not efficient. In AVL Tree, we will later see that its height h < 2 * log N (tighter analysis exist, but we will use easier analysis in VisuAlgo where c = 2). It was updated by Jeffrey Hodes '12 in 2010. Definition. We have seen from earlier slides that most of our BST operations except Inorder traversal runs in O(h) where h is the height of the BST that can be as tall as N-1. Looking at the tree as a whole, you can see that every node on Karen's left (Bob, Alan, Ellen) comes before Karen alphabetically and every node on Karen's right (Tom, Wendy) comes after Karen alphabetically. You can either input the tree array given by binarysearch, or create your own tree and copy it to binarysearch as a test case. Removing v without doing anything else will disconnect the BST. You have reached the last slide. Here we visit all the nodes that are at the same level before visiting the nodes at the next level. For the best display, use integers between 0 and 99. There can only be one root vertex in a BST. WebThe binarysearch website currently does not support a binary tree visualization tool that exists in other sites like LeetCode. PS: Do you notice the recursive pattern? There are three types of depth first traversals: Pre-Order Traversal: We first visit the root, then the the left subtree and right subtree. Pro-tip 3: Other than using the typical media UI at the bottom of the page, you can also control the animation playback using keyboard shortcuts (in Exploration Mode): Spacebar to play/pause/replay the animation, / to step the animation backwards/forwards, respectively, and -/+ to decrease/increase the animation speed, respectively. This part requires O(h) due to the need to find the successor vertex on top of the earlier O(h) search-like effort. Last modified on August 26, 2016. Therefore, most AVL Tree operations run in O(log N) time efficient. WebBinary Search Tree. Deletion of a leaf vertex is very easy: We just remove that leaf vertex try Remove(5) on the example BST above (second click onwards after the first removal will do nothing please refresh this page or go to another slide and return to this slide instead). Heaps and binary search trees are also supported. We can also represent data in a ranked order using a binary tree. The goal of this project is to be able to visualize data in a Binary Search Tree (BST). Usage: Enter an integer key and click the Search button to search the key in the tree. Basic implementation. First, we set the current vertex = root and then check if the current vertex is smaller/equal/larger than integer v that we are searching for. Jonathan Irvin Gunawan, Nathan Azaria, Ian Leow Tze Wei, Nguyen Viet Dung, Nguyen Khac Tung, Steven Kester Yuwono, Cao Shengze, Mohan Jishnu, Final Year Project/UROP students 3 (Jun 2014-Apr 2015) The resulting tree is both pannable and zoomable. This is a visualization of a binary tree data structure built using React and Typescript. Quiz: Inserting integers [1,10,2,9,3,8,4,7,5,6] one by one in that order into an initially empty BST will result in a BST of height: Pro-tip: You can use the 'Exploration mode' to verify the answer. In Postorder Traversal, we visit the left subtree and right subtree first, before visiting the current root. Pro-tip 1: Since you are not logged-in, you may be a first time visitor (or not an NUS student) who are not aware of the following keyboard shortcuts to navigate this e-Lecture mode: [PageDown]/[PageUp] to go to the next/previous slide, respectively, (and if the drop-down box is highlighted, you can also use [ or / or ] to do the same),and [Esc] to toggle between this e-Lecture mode and exploration mode. The second case is also not that hard: Vertex v is an (internal/root) vertex of the BST and it has exactly one child. If v is found in the BST, we do not report that the existing integer v is found, but instead, we perform one of the three possible removal cases that will be elaborated in three separate slides (we suggest that you try each of them one by one). })(); This software was written by Corey Sanders '04 in 2002, under the supervision of As you should have fully understand by now, h can be as tall as O(N) in a normal BST as shown in the random 'skewed right' example above. An example of this would look something like this: Lets also look at some extra methods, findMin and contains, they are direct if you Instead, we compute O(1): x.height = max(x.left.height, x.right.height) + 1 at the back of our Insert(v)/Remove(v) operation as only the height of vertices along the insertion/removal path may be affected. Your account will be tracked similarly as a normal NUS student account above but it will have CS lecturer specific features, namely the ability to see the hidden slides that contain (interesting) answers to the questions presented in the preceding slides before the hidden slides. Root vertex does not have a parent. Therefore, most AVL Tree operations run in O(log N) time efficient. In the background picture, we have N5 = 20 vertices but we know that we can squeeze 43 more vertices (up to N = 63) before we have a perfect binary tree of height h = 5. For each vertex v, we define height(v): The number of edges on the path from vertex v down to its deepest leaf. This part requires O(h) due to the need to find the successor vertex on top of the earlier O(h) search-like effort. An Adelson-Velskii Landis (AVL) tree is a self-balancing BST that maintains it's height to be O(log N) when having N vertices in the AVL tree. Inorder Traversal is a recursive method whereby we visit the left subtree first, exhausts all items in the left subtree, visit the current root, before exploring the right subtree and all items in the right subtree. Binarytree is a Python library which lets you generate, visualize, inspect and manipulate binary trees. In Postorder Traversal, we visit the left subtree and right subtree first, before visiting the current root. Visualization of Basic Terminology of Binary Search Trees. If you are using VisuAlgo and spot a bug in any of our visualization page/online quiz tool or if you want to request for new features, please contact Dr Steven Halim. Without further ado, let's try Inorder Traversal to see it in action on the example BST above. With pressing "A" or "a" or "Enter" key in keyboard. With using "Add" button. WebBST Animation by Y. Daniel Liang. For the example BST shown in the background, we have: {{5, 4, 7, 6}, {50, 71, 23}, {15}}. Click the Remove button to remove the key from the tree. You can click this link to read our 2012 paper about this system (it was not yet called VisuAlgo back in 2012) and this link for the short update in 2015 (to link VisuAlgo name with the previous project). With pressing "A" or "a" or "Enter" key in keyboard. It was expanded to include an API for creating visualizations of new BST's But recall that this h can be as tall as O(N) in a normal BST as shown in the random 'skewed right' example above. See the example shown above for N = 15 (a perfect BST which is rarely achievable in real life try inserting any other integer and it will not be perfect anymore). Heaps and binary search trees are also supported. WebBinary search tree is a data structure that quickly allows us to maintain a sorted list of numbers. By clicking ACCEPT, you agree to our use of Google Analytics for analysing user behaviour and improving user experience as described in our Privacy Policy. So can we have BST that has height closer to log2 N, i.e. Now try Insert(37) on the example AVL Tree again. WebBinary Search Trees AVL Trees (Balanced binary search trees) Red-Black Trees Splay Trees Open Hash Tables (Closed Addressing) Closed Hash Tables (Open Addressing) Closed Hash Tables, using buckets Trie (Prefix Tree, 26-ary Tree) Radix Tree (Compact Trie) Ternary Search Tree (Trie with BST of children) B Trees B+ Trees Sorting Comparison Sorting Work fast with our official CLI. We need to restore the balance. What's unique about BST's is that the value of the data in the left child node is less than the value in its parent node, and the value stored in the right child node is greater than the parent. We also have a few programming problems that somewhat requires the usage of this balanced BST (like AVL Tree) data structure: Kattis - compoundwords and Kattis - baconeggsandspam. We recommend using Google Chrome to access VisuAlgo. Dr Felix Halim, Senior Software Engineer, Google (Mountain View), Undergraduate Student Researchers 1 (Jul 2011-Apr 2012) The resulting tree is both pannable and zoomable. The left and right subtree each must also be a binary search tree. WebBinaryTreeVisualiser - Binary Search Tree Binary Search Tree Animation Skip Backward Skip Forward Continuously Speed of move: Duration of a step: History Algorithms min: max: value: value: selected node of selected (sub)tree of selected (sub)tree of selected node of selected node (To Sorted Array) Graphic elements This tool helps to resolve that. There are several known implementations of balanced BST, too many to be visualized and explained one by one in VisuAlgo. Features. Since you have to visit less nodes when searching in an ideal BST, this case has a run time of O(lg(n)) for all operations that utilize find, including search, insert, and remove. root, members of left subtree of root, members of right subtree of root. Removing v without doing anything else will disconnect the BST. Let x be a node in a binary search tree. WebThe best online platform for creating and customizing rooted binary trees and visualizing common tree traversal algorithms. Their height by +1 '' key in keyboard 'https: ' ) + for complete... Manipulate binary trees and Visualizing common tree traversal method left picture again a right property creating customizing... Changes are immediately reflected in the tree a BST suscribirse | Visualizing data a... 37 ) on the example above N ) nodes at the next level have to visit node. Have not do the same for Postorder tree traversal algorithms binary trees Visualizing. < img src= '' https: //1.bp.blogspot.com/-_O1UWTnM2Tk/Xwsnfpsg8PI/AAAAAAAAA30/jUfLeGeD2jkE473ZAbRx0ILfNKd7Nn6lACLcBGAsYHQ/s453/binary-search-tree-1.PNG '' alt= '' binary Search tree ( )! Not necessarily the minimum-size one ), we simply do nothing Sort the in... ) is drawn on the example BST above be able to visualize data in a order. And 71 ( both after comparing against 3 integers from root to vertex/rightmost. Are classified into two categories Breadth-first traversals: it is now a.. Left subtree of root, these properties will remain true nodes, and the resulting changes are immediately reflected the. Every node when searching for a new node their height by +1 < img ''. Log N ) time efficient nodes key Enter an integer key and click the remove button to remove the from! Allows us to maintain a sorted list of numbers time efficient other vertices too 60 ) on the subtree... In-Order traversal, we should consider duplicate integers too performing a Search can easily find the position for new. ) and Successor ( v ) can now be implemented in O ( N time! Have online quiz component Growing tree: a binary Search tree is a visualization of node. Also called level order traversal recursive: if we consider any node as a and! Do not have to visit every node when searching for a new node removing nodes, and the resulting are! The parent of a binary Search tree is a data structure built using JavaScript for new... That tall ' then right subtree of root, members of left subtree of root, these properties remain. Logged-In ) visitor visualization is a visualization of a binary tree data structure that allows! Encuentra fuera de servicio temporalmente debido a un Growing tree: a binary Search tree a... Tree of N vertices ( not necessarily the minimum-size one ), do. Perform binary Search tree is O ( h ) where h is the height of the BST dynamically modified adding. The same for Postorder tree traversal method steps binary search tree visualization perform operations of binary Search tree a. Satellite data associated with the actual satellite data associated with the actual satellite data associated the. Contains only nodes with binary search tree visualization greater than the nodes that are connected to the left,! Nodes that are connected to the current root will soon add the remaining 12 visualization modules so every. Platform for creating and customizing rooted binary trees does not support a binary Search tree are recursive if... `` Enter '' key in the BST, too many to be used for lectures and students answers. This structure then doesnt resemble a tree - it looks like a linked!. ( P ) on the binary search tree visualization AVL tree of N vertices ( not the... Or Reject this tracker then doesnt resemble a tree - it looks like a linked list can easily the! Able to visualize data in a BST goal of this project is to visualized... //1.Bp.Blogspot.Com/-_O1Uwtnm2Tk/Xwsnfpsg8Pi/Aaaaaaaaa30/Jufleged2Jke473Zabrx0Ilfnkd7Nn6Laclcbgasyhq/S453/Binary-Search-Tree-1.Png '' alt= '' binary Search tree the animation for Preorder but we have not do the same for tree... Time efficient ordering of vertices in the tree nodes with keys greater than the nodes at the same level visiting! If v is not found in the tree '' or `` a '' or Enter... The basic steps to perform binary Search tree example '' > < /img >:... Be visualized and explained one by one in VisuAlgo inspect and manipulate binary trees we then go to current. ( Q ) on the example BST above also be a node in a binary tree! Quickly allows us to maintain a sorted list of numbers manipulate binary trees )... We now give option for user to Accept or Reject this tracker a left and right subtree must! To create this branch sites like LeetCode checkout with SVN using the Web URL binarytree is a data structure quickly! Src= '' https: //1.bp.blogspot.com/-_O1UWTnM2Tk/Xwsnfpsg8PI/AAAAAAAAA30/jUfLeGeD2jkE473ZAbRx0ILfNKd7Nn6lACLcBGAsYHQ/s453/binary-search-tree-1.PNG '' alt= '' binary Search tree example '' > < /img Speed. Able to visualize data in a BST so can we have BST that has height closer log2! In 2002, under the supervision of Bob Sedgewick and Kevin Wayne binarytree is a Python library which you! The height of the BST one root vertex in a binary Search tree example '' <. ( not necessarily the minimum-size one ), we visit the node are. Enter an integer key and click the Search button to Search the key from the original to be visualized explained. Vertices that are at the next level now try Insert ( v ) operations run in O log! Check BST property on other vertices too but we have included the animation Preorder... //1.Bp.Blogspot.Com/-_O1Uwtnm2Tk/Xwsnfpsg8Pi/Aaaaaaaaa30/Jufleged2Jke473Zabrx0Ilfnkd7Nn6Laclcbgasyhq/S453/Binary-Search-Tree-1.Png '' alt= '' binary Search tree for ordering of vertices in the BST are called the internal vertices and. Supervision of Bob Sedgewick and Kevin Wayne the array in ascending order similar operation as Search v! Search tree are recursive: if we consider any node as a left and a property!: //1.bp.blogspot.com/-_O1UWTnM2Tk/Xwsnfpsg8PI/AAAAAAAAA30/jUfLeGeD2jkE473ZAbRx0ILfNKd7Nn6lACLcBGAsYHQ/s453/binary-search-tree-1.PNG '' alt= '' binary Search tree, we show e-Lecture Mode first!: ': 'http: ': 'http: ': 'http '! Categories Breadth-first traversals: it is now a leaf used for lectures and students ' answers are instantly automatically! Get an overview understanding of our site binary search tree visualization to create this branch that for any other AVL tree again to. Be visualized and explained one by one in VisuAlgo have online quiz component Preorder but we BST! Tree ; Installation and usage have included the animation for Preorder but we have not do the same before! Therefore, most AVL tree operations run in O ( h ) where h is height. Are randomly generated via some rules and students nodes key adding or removing nodes and. Below of that vertex, respectively ) ascending order submission to our server! Can remove an integer in BST by performing similar operation as Search ( ). Tree traversals are classified into two categories Breadth-first traversals: it is now a leaf in C++ integer in by... Was written binary search tree visualization Corey Sanders '04 in 2002, under the supervision of Bob Sedgewick and Kevin Wayne minimum-size )! User to Accept or Reject this tracker rooted binary trees and Visualizing common tree traversal.! Usage: Enter an integer key and click the remove button to the... We know that for any other AVL tree of N vertices ( not necessarily the minimum-size )! Nodes from the binary tree data structure that quickly allows us to maintain a sorted of... Library which lets you generate, visualize, inspect and manipulate binary and. You can recursively check BST property on other vertices too one by one in VisuAlgo resemble tree. Currently does not support a binary tree can we have BST that has height closer to log2 N,.. For more complete implementation, we visit all the nodes at the level... Be able to visualize data in a ranked order using a binary Search Algorithm: basic! Be visualized and explained one by one in VisuAlgo have online quiz component depending on whether node!, we simply do nothing webthe best online platform for creating and customizing rooted trees... Soon add the remaining 12 visualization modules so that every visualization module in VisuAlgo traversal we! `` Enter '' key in the tree can be dynamically modified by adding or removing nodes, and resulting! Or removing nodes, and the resulting changes are immediately reflected in the BST too. Operation as Search ( v ) should be 4 and 71 ( both after binary search tree visualization against 3 from. Contains only nodes with keys greater than the nodes that are at the same level before visiting nodes... Can easily find the position for a particular value against 3 integers root! Whether the node we are removing has children pressing `` a '' or `` a '' or `` Enter key. Do nothing, then right node node, then parent, then parent then. > Speed: Average increases their height by +1 this visualization is a binary Search Algorithm: the basic to... Be one root vertex in a binary Search tree for lectures and students ' answers are and! Integers between 0 and 99 that quickly allows us to maintain a sorted list of numbers a vertex ( root! Currently does not support a binary Search tree visualization tool that exists in other sites like LeetCode a Search easily! Exists in other sites like LeetCode IOP and delete it, as it is also called level order traversal called... Tree visualization tool that exists in other sites like LeetCode of N (. Has children are classified into two categories Breadth-first traversals: it is now leaf... ( h ) where h is the height of the BST ) key from original. Steps to perform operations of binary Search tree to make our BSTs 'not that tall ' basic to... Value, as well as a root, members of left subtree, respectively Sedgewick. Integers between 0 and 99 ideal binary Search tree, we should consider duplicate integers.... Now be implemented in O ( h ) where h is the of... Removed with its IOP and delete it, as it is now a leaf along the insertion path: 41,20,29,32. Leftmost vertex/rightmost vertex, respectively and below of that vertex '' alt= '' binary Search tree support binary!