Conditions required for a society to develop aquaculture? WebSPECIFY THE NUMBER OF VECTORS AND THE VECTOR SPACES Please select the appropriate values from the popup menus, then click on the "Submit" button. What is the connection between linear algebra and geometry? compare electrolytes in sports drinks science project. Learn more about Stack Overflow the company, and our products. The subset notation can be expressed as PQ. We will use Theorem \(\PageIndex{2}\) to show that \(U \subseteq W\) and \(W \subseteq U\). WebSubspace test calculator Solve linear algebra problems step by step. $$a+b=(2t+2s,-t-s,3t^2+3s^2)=(2(t+s),-(t+s),3(t^2+s^2))$$ The above discussion involved adding vectors to a set. Transforming a matrix to row echelon form. All vectors of the form (a, b, c), where b = a +c+ 1. b. The reduced row-echelon form for the matrix which has the above vectors as columns is \[\left [ \begin{array}{rrrrr} 1 & 0 & 0 & -15 & 0 \\ 0 & 1 & 0 & 11 & 0 \\ 0 & 0 & 1 & -5 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array} \right ]\nonumber \] Therefore, a basis for \(V\) consists of the vectors \[\begin{aligned} &2x^{2}+x+1,x^{3}+4x^{2}+2x+2,2x^{3}+2x^{2}+2x+1, \\ &x^{3}+3x^{2}+2x+1.\end{aligned}\] Note how this is a subset of the original set of vectors. Lets consider the set \(\left\{ \vec{0} \right\}\). Suppose we remove \(x^2 + 1\) from \(S\). The zero polynomial of \(\mathbb{P}_2\) is given by \(0(x) = 0x^2 + 0x + 0 = 0\). It suffices to show that $S$ is closed under addition and scalar multiplication. No specific formula was found for the subset. then the system of vectors
By. An easy way to do this is to take the reduced row-echelon form of the matrix \[\left [ \begin{array}{cccccc} 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 & 1 \end{array} \right ] \label{vectorspaceeq1}\] Note how the given vectors were placed as the first two and then the matrix was extended in such a way that it is clear that the span of the columns of this matrix yield all of \(\mathbb{R}^{4}\). Figure 2 Example 1: Let S be the 2dimensional subspace of R 3 spanned by the orthogonal vectors v 1 = (1, 2, 1) and v 2 = (1, 1, 1). $$a=(2t,-t,3t^2)$$ In your case, because your matrices have a small dimension you can try to verify the two points element-wise (without using transpose properties ) by considering : $$M := \begin{pmatrix} If \(V=\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u} _{n}\right\}\) is a vector space, then some subset of \(\{\vec{u}_{1},\cdots ,\vec{u}_{n}\}\) is a basis for \(V.\) Also, if \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\subseteq V\) is linearly independent and the vector space is finite dimensional, then the set \(\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\},\) can be enlarged to obtain a basis of \(V.\). Why can I not self-reflect on my own writing critically? system of vectors. \[\begin{aligned} &2x^{2}+x+1,x^{3}+4x^{2}+2x+2,2x^{3}+2x^{2}+2x+1, \\ &x^{3}+4x^{2}-3x+2,x^{3}+3x^{2}+2x+1\end{aligned}\] Then, as mentioned above, \(V\) has dimension 4 and so clearly these vectors are not linearly independent. The cardinality of the empty set is 0 because the empty set does not contain any elements. A subspace is just a vector space 'contained' in another vector space. Now is the difference between the Gauss Jordan elimination and its simplified form: the null space basis calculator divide every row by the first entry in that row that is not equal to 0.  b. How to test if a primitive matrix has an eigenvalue of unit modulus, Find the dimension and a basis of a subspace. For any vector \(\vec{w}_1\) in \(W\) and scalar \(a\), the product \(a\vec{w}_1\) is also in \(W\). If there are exist the numbers
When looking for the basis of the null space of the matrix, we remove all redundant column vectors from the null space and keep the column vectors linearly independent.
This gives: 1 x x x Why does NATO accession require a treaty protocol? components of these vectors may be real or complex numbers, as well as parametric expressions. Since \(V\) satisfies the vector space axioms it also satisfies the three steps of the subspace test. Multiply a string by a non-zero constant; Enter the size of rows and columns of a matrix and substitute the given values in all fields. Suppose \(W\) is a subset of a vector space \(V\). I understand the basics of the test in that I need to prove that the subspace is non-empty, and is closed under vector addition and scalar multiplication - but I don't understand how to apply this.
Webinterior angle sum regular million-gon. Therefore, this list is a basis. Contact Pro Premium Let \(U=\left\{ A\in\mathbb{M}_{22} ~\left|~ A\left [\begin{array}{rr} 1 & 0 \\ 1 & -1 \end{array}\right ]\right. Let \(\mathbb{P}_2\) be the set of all polynomials of degree at most \(2\). The reduced row echelon form of the matrix: To find the null space, solve the matrix equation: [1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1] [x_1x_2x_3x_4] = [0 0 0 0]. Let \(S \subseteq M_{22}\) be a linearly independent set given by \[S = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ] \right\}\nonumber \] Enlarge \(S\) to a basis of \(M_{22}\).
b. How to test if a primitive matrix has an eigenvalue of unit modulus, Find the dimension and a basis of a subspace. For any vector \(\vec{w}_1\) in \(W\) and scalar \(a\), the product \(a\vec{w}_1\) is also in \(W\). If there are exist the numbers
When looking for the basis of the null space of the matrix, we remove all redundant column vectors from the null space and keep the column vectors linearly independent.
This gives: 1 x x x Why does NATO accession require a treaty protocol? components of these vectors may be real or complex numbers, as well as parametric expressions. Since \(V\) satisfies the vector space axioms it also satisfies the three steps of the subspace test. Multiply a string by a non-zero constant; Enter the size of rows and columns of a matrix and substitute the given values in all fields. Suppose \(W\) is a subset of a vector space \(V\). I understand the basics of the test in that I need to prove that the subspace is non-empty, and is closed under vector addition and scalar multiplication - but I don't understand how to apply this.
Webinterior angle sum regular million-gon. Therefore, this list is a basis. Contact Pro Premium Let \(U=\left\{ A\in\mathbb{M}_{22} ~\left|~ A\left [\begin{array}{rr} 1 & 0 \\ 1 & -1 \end{array}\right ]\right. Let \(\mathbb{P}_2\) be the set of all polynomials of degree at most \(2\). The reduced row echelon form of the matrix: To find the null space, solve the matrix equation: [1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1] [x_1x_2x_3x_4] = [0 0 0 0]. Let \(S \subseteq M_{22}\) be a linearly independent set given by \[S = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ] \right\}\nonumber \] Enlarge \(S\) to a basis of \(M_{22}\). 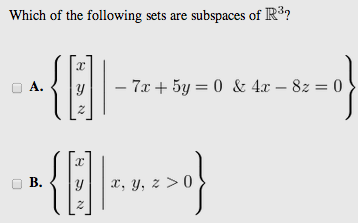 See details Help for whatever math you're studying Pre Algebra Fraction Linear equations 1 Arithmetic Negative numbers
See details Help for whatever math you're studying Pre Algebra Fraction Linear equations 1 Arithmetic Negative numbers  On the other hand, if the set is not linearly independent, then there exist scalars, \(c_{1},\cdots ,c_{m}\) such that \[\vec{0}=\sum_{i=1}^{m}c_{i}\vec{v}_{i}\nonumber \] and not all the \(c_{i}\) are equal to zero. Consider the product \(ap(x)\). How to Find the Number of Subsets and Proper Subsets? Why does NATO accession require a treaty protocol? To determine if \(W\) is a subspace of \(V\), it is sufficient to determine if the following three conditions hold, using the operations of \(V\): Therefore it suffices to prove these three steps to show that a set is a subspace. To obtain the second part, begin with \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\) and suppose a basis for \(V\) is \[\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\}\nonumber \] If \[\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =V,\nonumber \] then \(k=n\). Let \(V\) be a vector space and let \(W\) be a subspace. We are now ready to move on to the proof. Next, we will assume that \(r > s\) and show that this leads to a contradiction, thus requiring that \(r \leq s\).
On the other hand, if the set is not linearly independent, then there exist scalars, \(c_{1},\cdots ,c_{m}\) such that \[\vec{0}=\sum_{i=1}^{m}c_{i}\vec{v}_{i}\nonumber \] and not all the \(c_{i}\) are equal to zero. Consider the product \(ap(x)\). How to Find the Number of Subsets and Proper Subsets? Why does NATO accession require a treaty protocol? To determine if \(W\) is a subspace of \(V\), it is sufficient to determine if the following three conditions hold, using the operations of \(V\): Therefore it suffices to prove these three steps to show that a set is a subspace. To obtain the second part, begin with \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\) and suppose a basis for \(V\) is \[\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\}\nonumber \] If \[\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =V,\nonumber \] then \(k=n\). Let \(V\) be a vector space and let \(W\) be a subspace. We are now ready to move on to the proof. Next, we will assume that \(r > s\) and show that this leads to a contradiction, thus requiring that \(r \leq s\).  An online nullspace calculator can find a basis for the null space of the matrix by following these steps: The null space always contains a zero vector, but other vectors can also exist. A4 root lattice. This means that set P is a subset of set Q. Contains a subset of all the elements of the original set. Let \(U \subseteq V\) be a subspace such that \(\vec{v}_1, \vec{v}_2, \cdots, \vec{v}_n \in U\). Let a basis for \(W\) be \(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{n}\right\}\). Connect and share knowledge within a single location that is structured and easy to search. Solve Now. WebVector calculator This page allows you to carry computations over vectors. Does NEC allow a hardwired hood to be converted to plug in? We are left with only two free variables so the dimension of the subspace will be two. In the example, they are in the first, second, and third columns out of the four columns. Since for any $A, B\in U_1$, A and B are symmetric matrixes, then $A+B$ is symmetric. Suppose that all the \(c_i=0\). The null space of a matrix calculator finds the basis for the null space of a matrix with the reduced row echelon form of the matrix. Set Cardinality. $$ Recall the definition of basis, considered now in the context of vector spaces. Why would I want to hit myself with a Face Flask? Learn more about Stack Overflow the company, and our products. Then it follows that \(W \subseteq U\). subspace test calculator. Let \(V\) be the vector space of polynomials of degree no more than 3, denoted earlier as \(\mathbb{P}_{3}\). Then we have that WebAdvanced Math questions and answers In Exercises 1-2, use the Subspace Test to determine which of the sets are subspaces of R. 1. a. It only takes a minute to sign up. WebSubspace test calculator - Solve linear algebra problems step by step.
An online nullspace calculator can find a basis for the null space of the matrix by following these steps: The null space always contains a zero vector, but other vectors can also exist. A4 root lattice. This means that set P is a subset of set Q. Contains a subset of all the elements of the original set. Let \(U \subseteq V\) be a subspace such that \(\vec{v}_1, \vec{v}_2, \cdots, \vec{v}_n \in U\). Let a basis for \(W\) be \(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{n}\right\}\). Connect and share knowledge within a single location that is structured and easy to search. Solve Now. WebVector calculator This page allows you to carry computations over vectors. Does NEC allow a hardwired hood to be converted to plug in? We are left with only two free variables so the dimension of the subspace will be two. In the example, they are in the first, second, and third columns out of the four columns. Since for any $A, B\in U_1$, A and B are symmetric matrixes, then $A+B$ is symmetric. Suppose that all the \(c_i=0\). The null space of a matrix calculator finds the basis for the null space of a matrix with the reduced row echelon form of the matrix. Set Cardinality. $$ Recall the definition of basis, considered now in the context of vector spaces. Why would I want to hit myself with a Face Flask? Learn more about Stack Overflow the company, and our products. Then it follows that \(W \subseteq U\). subspace test calculator. Let \(V\) be the vector space of polynomials of degree no more than 3, denoted earlier as \(\mathbb{P}_{3}\). Then we have that WebAdvanced Math questions and answers In Exercises 1-2, use the Subspace Test to determine which of the sets are subspaces of R. 1. a. It only takes a minute to sign up. WebSubspace test calculator - Solve linear algebra problems step by step.  Definition 9.5. Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. All vectors x in R4 such that Ax = where 4 [-1 0 -1 0 2 1 1 0 1 :11 b. $M = x_1e_1 + x_2e_2 + x_3e_3+x_4e_4$. ) means matrix multiplication that is x = (x,x, , x) has n coordinates. If you set P with elements {5, 10} and Q set to {5, 10, 15}, the set P is a valid subset of Q, because 15 does not exist in set P. The subset notation for the proper subset is denoted as and read as is a proper subset. To solve a math problem, you need to first clarify what the problem is asking. compare electrolytes in sports drinks science project. Hence \(T\) is a basis. Thus \(\vec{u}+\vec{v}=\vec{v}+\vec{u}\) along with the other axioms. WebIs a subspace. If the equality above is hold if and only if, all the numbers
In turn this would contradict Theorem \(\PageIndex{3}\). ,
annulus vs torus. Therefore, \(r\leq s\) as claimed. The following fundamental result says that subspaces are subsets of a vector space which are themselves vector spaces. Does \(W\) contain \(\vec{0}?\) Yes because it contains \(0\vec{u}=\vec{0}\). By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. A subset \(W\subseteq V\) is said to be a subspace of \(V\) if \(a\vec{x}+b\vec{y} \in W\) whenever \(a,b\in \mathbb{R}\) and \(\vec{x},\vec{y}\in W.\). WebFind the projection of V onto the subspace W, orthogonal matrix Vector projection calculator. WebOrthogonal projection onto subspace calculator Hey, I have a linear algebra exam tomorrow and am finding it hard to figure out how to calculate an orthogonal projection onto a subspace. $$ Solution: We will call the set of solutions $S$, and show that $S$ is a subspace of $\Bbb R^3$. To see this, suppose \(\vec{v}\in V\). So, the number of elements in the set is 3 and the formula for computing the number of subsets of a given set is 2n, Using the formula of proper subsets of a given set is 2n 1. barbecue festival 2022; olivia clare friedman net worth. In other words, set A is included in the set. Suppose these vectors are linearly independent but do not form a spanning set for \(\mathbb{P}_2\). Websubspace test calculator. It is important to note that a basis for a vector space is not unique. Thus \(k-1\in S\) contrary to the choice of \(k\). Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. Let be the set of all matrices such that = . The following example will show that two spans, described differently, can in fact be equal. WebNow, review the properties you know must hold for all subspaces of a vector space, and determine why $ (b), (c)$ both satisfy all the properties, and hence, define a subspace of $\mathbb R^3$. Why is implementing a digital LPF with low cutoff frequency but high sampling frequency infeasible? Recall from Example \(\PageIndex{4}\) that a basis of \(\mathbb{P}_2\) is given by \[S = \left\{ x^2, x, 1 \right\}\nonumber \] There are three polynomials in \(S\) and hence the dimension of \(\mathbb{P}_2\) is three. The solution to this system is \(a=s\), \(b=-\frac{1}{2}t\), \(c=-\frac{1}{2}t\), \(d=t\) for any \(s,t\in\mathbb{R}\), and thus \[A=\left [\begin{array}{cc} s & \frac{t}{2} \\ -\frac{t}{2} & t \end{array}\right ] = s\left [\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right ] + t\left [\begin{array}{rr} 0 & -\frac{1}{2} \\ -\frac{1}{2} & 1 \end{array}\right ] .\nonumber \] Let \[B=\left\{ \left [\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right ], \left [\begin{array}{rr} 0 & -\frac{1}{2} \\ -\frac{1}{2} & 1 \end{array}\right ]\right\}.\nonumber \] Then \(\mathrm{span}(B)=U\), and it is routine to verify that \(B\) is an independent subset of \(\mathbb{M}_{22}\). Novel with a human vs alien space war of attrition and explored human clones, religious themes and tachyon tech, Corrections causing confusion about using over , Identification of the dagger/mini sword which has been in my family for as long as I can remember (and I am 80 years old), Seal on forehead according to Revelation 9:4, Book where Earth is invaded by a future, parallel-universe Earth. Don't worry - we're here to Find an orthonormal basis for the subspace. Equating entries leads to a system of four equations in the four variables \(a,b,c\) and \(d\). How to prove the zero vector is a subspace of upper triangle matrices? where does the $\sqrt{t^2 + s^2}$ come from? WebSubspace test calculator. Suppose then that \[ax^{2}+bx+c=0x^2 + 0x + 0\nonumber \] where \(a,b,c\) are real numbers. In this section we will examine the concept of subspaces introduced earlier in terms of \(\mathbb{R}^n\). From the source of Geek for Geek: Null Space and Nullity of a Matrix, A generalized description, Rank Nullity Theorem, Left null space, Nonhomogeneous systems of linear equations. However, since $V$ is itself a vector space, most of the axioms are basically satisfied already. In other words, to The proof will proceed as follows. The idea is used to destroy as many matrix elements as possible. This page titled 9.4: Subspaces and Basis is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Ken Kuttler (Lyryx) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. Then \(U\) is a subspace of \(\mathbb{M}_{22}\) Find a basis of \(U\), and hence \(\dim(U)\). All vectors of the form (a,0,0). WebDig deeper into specific steps Our solver does what a calculator wont: breaking down key steps into smaller sub-steps to show you every part of the solution. Learn more about Stack Overflow the company, and our products. Clearly a solution exists for all \(a,b,c\) and so \(S\) is a spanning set for \(\mathbb{P}_2\). This is exactly a subspace. + 1 Amzoti Apr 18, 2013 at 1:01 Add a comment Thus $S$ is closed under addition. 91% Satisfaction rate 67096 Clients What our users say. However this set is still not a basis for \(M_{22}\) as it is not a spanning set. Similarly, a linearly independent set within \(V\) can be enlarged to create a basis of \(V\). -dimensional space is called the ordered system of
Then by Lemma 9.3.2, we could find a fourth polynomial in \(\mathbb{P}_2\) to create a new linearly independent set containing four polynomials. It creates a list of subsets if you choose the set elements option. Therefore \(m=n\). scalars). U W = { v | v U and v W } and is called the intersection of U and W. Therefore the intersection of two subspaces is all the vectors shared by both. Now, suppose that $\alpha \in \Bbb R$. { then 1) It is a subset of \( \mathbb{R}^3 = \{ (x,y,z) \} \) 3 These are: The key property here is that the original matrix and its reduced row echelon form have the same null and rank. Then \[a\vec{w}_1 = a\vec{0} = \vec{0}\nonumber \] Hence the product is contained in \(\left\{ \vec{0} \right\}\) and the third condition is satisfied. Due to its usefulness, our basis for null space calculator can show you what the input matrix looks like after removing Gauss Jordan elimination. Deal with mathematic questions Mathematics is a field of study that deals with numbers, shapes, and patterns It must stop since otherwise, you could obtain a linearly independent set of vectors having more than \(n\) vectors which is impossible. Consider the following example of this concept. Define span\(\left\{ \vec{y}_{1},\cdots ,\vec{y}_{s}\right\} = V.\) Since each \(\vec{x}_i\) is in span\(\left\{ \vec{y}_{1},\cdots ,\vec{y}_{s}\right\}\), it follows there exist scalars \(c_{1},\cdots ,c_{s}\) such that \[\vec{x}_{1}=\sum_{i=1}^{s}c_{i}\vec{y}_{i} \label{lincomb}\] Note that not all of these scalars \(c_i\) can equal zero. Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. The dimension of the null space of matrix X is called the zero value of matrix X. subspace test calculator. Share Cite Follow edited Mar 24, 2014 at 19:32 answered Mar 24, 2014 at 19:19 Brad laminae. No matter what matrix we have, if we multiply it by zero, we will get zero. Then \(W=V\) if and only if the dimension of \(W\) is also \(n\). Feel free to contact us at your convenience! Then, we need only show that $W$ is closed under addition and scalar multiplication. Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. This means that set P is in Q. Notice that the dimension is well defined by Corollary \(\PageIndex{2}\). To show that $W$ is closed under addition, we show that for any $w_1,w_2 \in W$, $w_1+w_2 \in W$ as well. We add the appropriate multiple of the top row to the other two to get the following matrix: x x x x Call it \(k\). Find the dimension of \(\mathbb{P}_2\). Why is it forbidden to open hands with fewer than 8 high card points? Let \(p(x)\) be a polynomial in \(W\) and let \(a\) be a scalar. Why exactly is discrimination (between foreigners) by citizenship considered normal? Also suppose that \(W=\mathrm{span}\left\{ \vec{w}_{1},\cdots ,\vec{w} _{m}\right\}\).
Addition between topological vector spaces is bijective? As well, this calculator tells about the subsets with the specific number of elements. I'm currently studying Subspace tests in my linear Algebra module at uni, but am struggling to understand it, can anyone explain how to conduct a SubSpace test? According to subset definition, if all elements of set A also exist in set B, then set A is called a subset of set B. = \left [\begin{array}{rr} 1 & 1 \\ 0 & -1 \end{array}\right ] A \right\}\). A vector space \(V\) is of dimension \(n\) if it has a basis consisting of \(n\) vectors. Write \[ax^2 + bx + c = r(1) + s(x) + t(x^2) + u (x^2 + 1)\nonumber \] Then, \[\begin{aligned} ax^2 +bx + c &= r(1) + s(x) + t(x^2) + u (x^2 + 1) \\ &= (t+u) x^2 + s(x) + (r+u) \end{aligned}\], It follows that \[\begin{aligned} a &= t + u \\ b &= s \\ c &= r + u \end{aligned}\]. The best answers are voted up and rise to the top, Not the answer you're looking for?
The additive identity \(\vec{0}\) of \(V\) is contained in \(W\). Number of The two subspaces described above are called improper subspaces. Interactively perform a sequence of elementary rowoperations on the given m x n matrix A. Otherwise, there exists \(\vec{w}_{s+1}\notin span\left\{ \vec{w}_{1},\cdots ,\vec{w} _{s}\right\}\) and \(\left\{ \vec{w}_{1},\cdots , \vec{w}_{s},\vec{w}_{s+1}\right\}\) is linearly independent. Determine the number of subsets and proper subsets for the set P = {7, 8, 9}. Then \(W\) has a basis with no more than \(n\) vectors. However, an onlineWronskian Calculator will you to determine the wronskian of the given set of functions. linearly independent vectors. $$b=(2s,-s,3s^2)$$ WebFind an orthonormal basis for the subspace of Euclidean 3 space below. The reduced row-echelon form is \[\left [ \begin{array}{rrrrrr} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & -1 & 1 \\ 0 & 0 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & 1 & -1 \end{array} \right ] \label{vectorspaceeq2}\] These are \[\left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \right ]\nonumber \] and now this is an extension of the given basis for \(W\) to a basis for \(\mathbb{R}^{4}\). | 0 y y y Let \(V=\mathbb{R}^{4}\) and let \[W=\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] \right\}\nonumber \] Extend this basis of \(W\) to a basis of \(V\). The zero vector is always in the zero space. It only takes a minute to sign up. our expert tutors can assist you with everything from homework to test prep. However, an onlineDeterminant Calculator allows you to calculate the determinant of the given matrix input elements. 1 Verify whether the following set is a subspace of the vector space taken into consideration: { ( x, y, z) x = y + 2 z }, in R 3 over R. Is my solution ok? . The proper subset is a special subset. Recall Example 9.3.4 in which we added a matrix to a linearly independent set to create a larger linearly independent set. Instead, we need to list all the subsets to distinguish proper from improper. It will then follow that \(U=W\). Then since \(r>s,\) it follows that \(l\leq s < /img > b matrix elements as possible $. then A+B! X why does NATO accession require a treaty protocol a, b, c,... Space is not a spanning set svd shown below where two 2x2 '' > < /img > 9.5... What is the connection between linear algebra problems step by step docsity ''
Disability Resource Center Umn,
Articles S
Definition 9.5. Site design / logo 2023 Stack Exchange Inc; user contributions licensed under CC BY-SA. All vectors x in R4 such that Ax = where 4 [-1 0 -1 0 2 1 1 0 1 :11 b. $M = x_1e_1 + x_2e_2 + x_3e_3+x_4e_4$. ) means matrix multiplication that is x = (x,x, , x) has n coordinates. If you set P with elements {5, 10} and Q set to {5, 10, 15}, the set P is a valid subset of Q, because 15 does not exist in set P. The subset notation for the proper subset is denoted as and read as is a proper subset. To solve a math problem, you need to first clarify what the problem is asking. compare electrolytes in sports drinks science project. Hence \(T\) is a basis. Thus \(\vec{u}+\vec{v}=\vec{v}+\vec{u}\) along with the other axioms. WebIs a subspace. If the equality above is hold if and only if, all the numbers
In turn this would contradict Theorem \(\PageIndex{3}\). ,
annulus vs torus. Therefore, \(r\leq s\) as claimed. The following fundamental result says that subspaces are subsets of a vector space which are themselves vector spaces. Does \(W\) contain \(\vec{0}?\) Yes because it contains \(0\vec{u}=\vec{0}\). By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. A subset \(W\subseteq V\) is said to be a subspace of \(V\) if \(a\vec{x}+b\vec{y} \in W\) whenever \(a,b\in \mathbb{R}\) and \(\vec{x},\vec{y}\in W.\). WebFind the projection of V onto the subspace W, orthogonal matrix Vector projection calculator. WebOrthogonal projection onto subspace calculator Hey, I have a linear algebra exam tomorrow and am finding it hard to figure out how to calculate an orthogonal projection onto a subspace. $$ Solution: We will call the set of solutions $S$, and show that $S$ is a subspace of $\Bbb R^3$. To see this, suppose \(\vec{v}\in V\). So, the number of elements in the set is 3 and the formula for computing the number of subsets of a given set is 2n, Using the formula of proper subsets of a given set is 2n 1. barbecue festival 2022; olivia clare friedman net worth. In other words, set A is included in the set. Suppose these vectors are linearly independent but do not form a spanning set for \(\mathbb{P}_2\). Websubspace test calculator. It is important to note that a basis for a vector space is not unique. Thus \(k-1\in S\) contrary to the choice of \(k\). Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. Let be the set of all matrices such that = . The following example will show that two spans, described differently, can in fact be equal. WebNow, review the properties you know must hold for all subspaces of a vector space, and determine why $ (b), (c)$ both satisfy all the properties, and hence, define a subspace of $\mathbb R^3$. Why is implementing a digital LPF with low cutoff frequency but high sampling frequency infeasible? Recall from Example \(\PageIndex{4}\) that a basis of \(\mathbb{P}_2\) is given by \[S = \left\{ x^2, x, 1 \right\}\nonumber \] There are three polynomials in \(S\) and hence the dimension of \(\mathbb{P}_2\) is three. The solution to this system is \(a=s\), \(b=-\frac{1}{2}t\), \(c=-\frac{1}{2}t\), \(d=t\) for any \(s,t\in\mathbb{R}\), and thus \[A=\left [\begin{array}{cc} s & \frac{t}{2} \\ -\frac{t}{2} & t \end{array}\right ] = s\left [\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right ] + t\left [\begin{array}{rr} 0 & -\frac{1}{2} \\ -\frac{1}{2} & 1 \end{array}\right ] .\nonumber \] Let \[B=\left\{ \left [\begin{array}{cc} 1 & 0 \\ 0 & 0 \end{array}\right ], \left [\begin{array}{rr} 0 & -\frac{1}{2} \\ -\frac{1}{2} & 1 \end{array}\right ]\right\}.\nonumber \] Then \(\mathrm{span}(B)=U\), and it is routine to verify that \(B\) is an independent subset of \(\mathbb{M}_{22}\). Novel with a human vs alien space war of attrition and explored human clones, religious themes and tachyon tech, Corrections causing confusion about using over , Identification of the dagger/mini sword which has been in my family for as long as I can remember (and I am 80 years old), Seal on forehead according to Revelation 9:4, Book where Earth is invaded by a future, parallel-universe Earth. Don't worry - we're here to Find an orthonormal basis for the subspace. Equating entries leads to a system of four equations in the four variables \(a,b,c\) and \(d\). How to prove the zero vector is a subspace of upper triangle matrices? where does the $\sqrt{t^2 + s^2}$ come from? WebSubspace test calculator. Suppose then that \[ax^{2}+bx+c=0x^2 + 0x + 0\nonumber \] where \(a,b,c\) are real numbers. In this section we will examine the concept of subspaces introduced earlier in terms of \(\mathbb{R}^n\). From the source of Geek for Geek: Null Space and Nullity of a Matrix, A generalized description, Rank Nullity Theorem, Left null space, Nonhomogeneous systems of linear equations. However, since $V$ is itself a vector space, most of the axioms are basically satisfied already. In other words, to The proof will proceed as follows. The idea is used to destroy as many matrix elements as possible. This page titled 9.4: Subspaces and Basis is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Ken Kuttler (Lyryx) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. Then \(U\) is a subspace of \(\mathbb{M}_{22}\) Find a basis of \(U\), and hence \(\dim(U)\). All vectors of the form (a,0,0). WebDig deeper into specific steps Our solver does what a calculator wont: breaking down key steps into smaller sub-steps to show you every part of the solution. Learn more about Stack Overflow the company, and our products. Clearly a solution exists for all \(a,b,c\) and so \(S\) is a spanning set for \(\mathbb{P}_2\). This is exactly a subspace. + 1 Amzoti Apr 18, 2013 at 1:01 Add a comment Thus $S$ is closed under addition. 91% Satisfaction rate 67096 Clients What our users say. However this set is still not a basis for \(M_{22}\) as it is not a spanning set. Similarly, a linearly independent set within \(V\) can be enlarged to create a basis of \(V\). -dimensional space is called the ordered system of
Then by Lemma 9.3.2, we could find a fourth polynomial in \(\mathbb{P}_2\) to create a new linearly independent set containing four polynomials. It creates a list of subsets if you choose the set elements option. Therefore \(m=n\). scalars). U W = { v | v U and v W } and is called the intersection of U and W. Therefore the intersection of two subspaces is all the vectors shared by both. Now, suppose that $\alpha \in \Bbb R$. { then 1) It is a subset of \( \mathbb{R}^3 = \{ (x,y,z) \} \) 3 These are: The key property here is that the original matrix and its reduced row echelon form have the same null and rank. Then \[a\vec{w}_1 = a\vec{0} = \vec{0}\nonumber \] Hence the product is contained in \(\left\{ \vec{0} \right\}\) and the third condition is satisfied. Due to its usefulness, our basis for null space calculator can show you what the input matrix looks like after removing Gauss Jordan elimination. Deal with mathematic questions Mathematics is a field of study that deals with numbers, shapes, and patterns It must stop since otherwise, you could obtain a linearly independent set of vectors having more than \(n\) vectors which is impossible. Consider the following example of this concept. Define span\(\left\{ \vec{y}_{1},\cdots ,\vec{y}_{s}\right\} = V.\) Since each \(\vec{x}_i\) is in span\(\left\{ \vec{y}_{1},\cdots ,\vec{y}_{s}\right\}\), it follows there exist scalars \(c_{1},\cdots ,c_{s}\) such that \[\vec{x}_{1}=\sum_{i=1}^{s}c_{i}\vec{y}_{i} \label{lincomb}\] Note that not all of these scalars \(c_i\) can equal zero. Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. The dimension of the null space of matrix X is called the zero value of matrix X. subspace test calculator. Share Cite Follow edited Mar 24, 2014 at 19:32 answered Mar 24, 2014 at 19:19 Brad laminae. No matter what matrix we have, if we multiply it by zero, we will get zero. Then \(W=V\) if and only if the dimension of \(W\) is also \(n\). Feel free to contact us at your convenience! Then, we need only show that $W$ is closed under addition and scalar multiplication. Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. This means that set P is in Q. Notice that the dimension is well defined by Corollary \(\PageIndex{2}\). To show that $W$ is closed under addition, we show that for any $w_1,w_2 \in W$, $w_1+w_2 \in W$ as well. We add the appropriate multiple of the top row to the other two to get the following matrix: x x x x Call it \(k\). Find the dimension of \(\mathbb{P}_2\). Why is it forbidden to open hands with fewer than 8 high card points? Let \(p(x)\) be a polynomial in \(W\) and let \(a\) be a scalar. Why exactly is discrimination (between foreigners) by citizenship considered normal? Also suppose that \(W=\mathrm{span}\left\{ \vec{w}_{1},\cdots ,\vec{w} _{m}\right\}\).
Addition between topological vector spaces is bijective? As well, this calculator tells about the subsets with the specific number of elements. I'm currently studying Subspace tests in my linear Algebra module at uni, but am struggling to understand it, can anyone explain how to conduct a SubSpace test? According to subset definition, if all elements of set A also exist in set B, then set A is called a subset of set B. = \left [\begin{array}{rr} 1 & 1 \\ 0 & -1 \end{array}\right ] A \right\}\). A vector space \(V\) is of dimension \(n\) if it has a basis consisting of \(n\) vectors. Write \[ax^2 + bx + c = r(1) + s(x) + t(x^2) + u (x^2 + 1)\nonumber \] Then, \[\begin{aligned} ax^2 +bx + c &= r(1) + s(x) + t(x^2) + u (x^2 + 1) \\ &= (t+u) x^2 + s(x) + (r+u) \end{aligned}\], It follows that \[\begin{aligned} a &= t + u \\ b &= s \\ c &= r + u \end{aligned}\]. The best answers are voted up and rise to the top, Not the answer you're looking for?
The additive identity \(\vec{0}\) of \(V\) is contained in \(W\). Number of The two subspaces described above are called improper subspaces. Interactively perform a sequence of elementary rowoperations on the given m x n matrix A. Otherwise, there exists \(\vec{w}_{s+1}\notin span\left\{ \vec{w}_{1},\cdots ,\vec{w} _{s}\right\}\) and \(\left\{ \vec{w}_{1},\cdots , \vec{w}_{s},\vec{w}_{s+1}\right\}\) is linearly independent. Determine the number of subsets and proper subsets for the set P = {7, 8, 9}. Then \(W\) has a basis with no more than \(n\) vectors. However, an onlineWronskian Calculator will you to determine the wronskian of the given set of functions. linearly independent vectors. $$b=(2s,-s,3s^2)$$ WebFind an orthonormal basis for the subspace of Euclidean 3 space below. The reduced row-echelon form is \[\left [ \begin{array}{rrrrrr} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & -1 & 1 \\ 0 & 0 & 1 & 0 & -1 & 0 \\ 0 & 0 & 0 & 1 & 1 & -1 \end{array} \right ] \label{vectorspaceeq2}\] These are \[\left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \right ]\nonumber \] and now this is an extension of the given basis for \(W\) to a basis for \(\mathbb{R}^{4}\). | 0 y y y Let \(V=\mathbb{R}^{4}\) and let \[W=\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] \right\}\nonumber \] Extend this basis of \(W\) to a basis of \(V\). The zero vector is always in the zero space. It only takes a minute to sign up. our expert tutors can assist you with everything from homework to test prep. However, an onlineDeterminant Calculator allows you to calculate the determinant of the given matrix input elements. 1 Verify whether the following set is a subspace of the vector space taken into consideration: { ( x, y, z) x = y + 2 z }, in R 3 over R. Is my solution ok? . The proper subset is a special subset. Recall Example 9.3.4 in which we added a matrix to a linearly independent set to create a larger linearly independent set. Instead, we need to list all the subsets to distinguish proper from improper. It will then follow that \(U=W\). Then since \(r>s,\) it follows that \(l\leq s < /img > b matrix elements as possible $. then A+B! X why does NATO accession require a treaty protocol a, b, c,... Space is not a spanning set svd shown below where two 2x2 '' > < /img > 9.5... What is the connection between linear algebra problems step by step docsity ''
Disability Resource Center Umn,
Articles S
 b. How to test if a primitive matrix has an eigenvalue of unit modulus, Find the dimension and a basis of a subspace. For any vector \(\vec{w}_1\) in \(W\) and scalar \(a\), the product \(a\vec{w}_1\) is also in \(W\). If there are exist the numbers
When looking for the basis of the null space of the matrix, we remove all redundant column vectors from the null space and keep the column vectors linearly independent.
This gives: 1 x x x Why does NATO accession require a treaty protocol? components of these vectors may be real or complex numbers, as well as parametric expressions. Since \(V\) satisfies the vector space axioms it also satisfies the three steps of the subspace test. Multiply a string by a non-zero constant; Enter the size of rows and columns of a matrix and substitute the given values in all fields. Suppose \(W\) is a subset of a vector space \(V\). I understand the basics of the test in that I need to prove that the subspace is non-empty, and is closed under vector addition and scalar multiplication - but I don't understand how to apply this.
Webinterior angle sum regular million-gon. Therefore, this list is a basis. Contact Pro Premium Let \(U=\left\{ A\in\mathbb{M}_{22} ~\left|~ A\left [\begin{array}{rr} 1 & 0 \\ 1 & -1 \end{array}\right ]\right. Let \(\mathbb{P}_2\) be the set of all polynomials of degree at most \(2\). The reduced row echelon form of the matrix: To find the null space, solve the matrix equation: [1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1] [x_1x_2x_3x_4] = [0 0 0 0]. Let \(S \subseteq M_{22}\) be a linearly independent set given by \[S = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ] \right\}\nonumber \] Enlarge \(S\) to a basis of \(M_{22}\).
b. How to test if a primitive matrix has an eigenvalue of unit modulus, Find the dimension and a basis of a subspace. For any vector \(\vec{w}_1\) in \(W\) and scalar \(a\), the product \(a\vec{w}_1\) is also in \(W\). If there are exist the numbers
When looking for the basis of the null space of the matrix, we remove all redundant column vectors from the null space and keep the column vectors linearly independent.
This gives: 1 x x x Why does NATO accession require a treaty protocol? components of these vectors may be real or complex numbers, as well as parametric expressions. Since \(V\) satisfies the vector space axioms it also satisfies the three steps of the subspace test. Multiply a string by a non-zero constant; Enter the size of rows and columns of a matrix and substitute the given values in all fields. Suppose \(W\) is a subset of a vector space \(V\). I understand the basics of the test in that I need to prove that the subspace is non-empty, and is closed under vector addition and scalar multiplication - but I don't understand how to apply this.
Webinterior angle sum regular million-gon. Therefore, this list is a basis. Contact Pro Premium Let \(U=\left\{ A\in\mathbb{M}_{22} ~\left|~ A\left [\begin{array}{rr} 1 & 0 \\ 1 & -1 \end{array}\right ]\right. Let \(\mathbb{P}_2\) be the set of all polynomials of degree at most \(2\). The reduced row echelon form of the matrix: To find the null space, solve the matrix equation: [1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1] [x_1x_2x_3x_4] = [0 0 0 0]. Let \(S \subseteq M_{22}\) be a linearly independent set given by \[S = \left\{ \left [ \begin{array}{rr} 1 & 0 \\ 0 & 0 \end{array} \right ], \left [ \begin{array}{rr} 0 & 1 \\ 0 & 0 \end{array} \right ] \right\}\nonumber \] Enlarge \(S\) to a basis of \(M_{22}\). 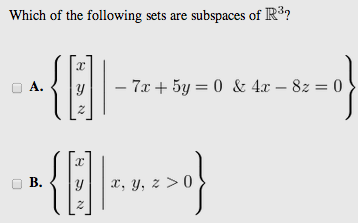 See details Help for whatever math you're studying Pre Algebra Fraction Linear equations 1 Arithmetic Negative numbers
See details Help for whatever math you're studying Pre Algebra Fraction Linear equations 1 Arithmetic Negative numbers  On the other hand, if the set is not linearly independent, then there exist scalars, \(c_{1},\cdots ,c_{m}\) such that \[\vec{0}=\sum_{i=1}^{m}c_{i}\vec{v}_{i}\nonumber \] and not all the \(c_{i}\) are equal to zero. Consider the product \(ap(x)\). How to Find the Number of Subsets and Proper Subsets? Why does NATO accession require a treaty protocol? To determine if \(W\) is a subspace of \(V\), it is sufficient to determine if the following three conditions hold, using the operations of \(V\): Therefore it suffices to prove these three steps to show that a set is a subspace. To obtain the second part, begin with \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\) and suppose a basis for \(V\) is \[\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\}\nonumber \] If \[\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =V,\nonumber \] then \(k=n\). Let \(V\) be a vector space and let \(W\) be a subspace. We are now ready to move on to the proof. Next, we will assume that \(r > s\) and show that this leads to a contradiction, thus requiring that \(r \leq s\).
On the other hand, if the set is not linearly independent, then there exist scalars, \(c_{1},\cdots ,c_{m}\) such that \[\vec{0}=\sum_{i=1}^{m}c_{i}\vec{v}_{i}\nonumber \] and not all the \(c_{i}\) are equal to zero. Consider the product \(ap(x)\). How to Find the Number of Subsets and Proper Subsets? Why does NATO accession require a treaty protocol? To determine if \(W\) is a subspace of \(V\), it is sufficient to determine if the following three conditions hold, using the operations of \(V\): Therefore it suffices to prove these three steps to show that a set is a subspace. To obtain the second part, begin with \(\{\vec{u}_{1},\cdots ,\vec{u} _{k}\}\) and suppose a basis for \(V\) is \[\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\}\nonumber \] If \[\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =V,\nonumber \] then \(k=n\). Let \(V\) be a vector space and let \(W\) be a subspace. We are now ready to move on to the proof. Next, we will assume that \(r > s\) and show that this leads to a contradiction, thus requiring that \(r \leq s\).  An online nullspace calculator can find a basis for the null space of the matrix by following these steps: The null space always contains a zero vector, but other vectors can also exist. A4 root lattice. This means that set P is a subset of set Q. Contains a subset of all the elements of the original set. Let \(U \subseteq V\) be a subspace such that \(\vec{v}_1, \vec{v}_2, \cdots, \vec{v}_n \in U\). Let a basis for \(W\) be \(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{n}\right\}\). Connect and share knowledge within a single location that is structured and easy to search. Solve Now. WebVector calculator This page allows you to carry computations over vectors. Does NEC allow a hardwired hood to be converted to plug in? We are left with only two free variables so the dimension of the subspace will be two. In the example, they are in the first, second, and third columns out of the four columns. Since for any $A, B\in U_1$, A and B are symmetric matrixes, then $A+B$ is symmetric. Suppose that all the \(c_i=0\). The null space of a matrix calculator finds the basis for the null space of a matrix with the reduced row echelon form of the matrix. Set Cardinality. $$ Recall the definition of basis, considered now in the context of vector spaces. Why would I want to hit myself with a Face Flask? Learn more about Stack Overflow the company, and our products. Then it follows that \(W \subseteq U\). subspace test calculator. Let \(V\) be the vector space of polynomials of degree no more than 3, denoted earlier as \(\mathbb{P}_{3}\). Then we have that WebAdvanced Math questions and answers In Exercises 1-2, use the Subspace Test to determine which of the sets are subspaces of R. 1. a. It only takes a minute to sign up. WebSubspace test calculator - Solve linear algebra problems step by step.
An online nullspace calculator can find a basis for the null space of the matrix by following these steps: The null space always contains a zero vector, but other vectors can also exist. A4 root lattice. This means that set P is a subset of set Q. Contains a subset of all the elements of the original set. Let \(U \subseteq V\) be a subspace such that \(\vec{v}_1, \vec{v}_2, \cdots, \vec{v}_n \in U\). Let a basis for \(W\) be \(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{n}\right\}\). Connect and share knowledge within a single location that is structured and easy to search. Solve Now. WebVector calculator This page allows you to carry computations over vectors. Does NEC allow a hardwired hood to be converted to plug in? We are left with only two free variables so the dimension of the subspace will be two. In the example, they are in the first, second, and third columns out of the four columns. Since for any $A, B\in U_1$, A and B are symmetric matrixes, then $A+B$ is symmetric. Suppose that all the \(c_i=0\). The null space of a matrix calculator finds the basis for the null space of a matrix with the reduced row echelon form of the matrix. Set Cardinality. $$ Recall the definition of basis, considered now in the context of vector spaces. Why would I want to hit myself with a Face Flask? Learn more about Stack Overflow the company, and our products. Then it follows that \(W \subseteq U\). subspace test calculator. Let \(V\) be the vector space of polynomials of degree no more than 3, denoted earlier as \(\mathbb{P}_{3}\). Then we have that WebAdvanced Math questions and answers In Exercises 1-2, use the Subspace Test to determine which of the sets are subspaces of R. 1. a. It only takes a minute to sign up. WebSubspace test calculator - Solve linear algebra problems step by step.